What is adaptive learning?

And how can adaptive technology create personalized learning experiences for students?

Adaptive learning is not a new concept, but its implementation is now finally becoming a reality and those in the education sector should know what it is so they can be ready to benefit from it.

So what is adaptive learning?

Adaptive learning is the use of technology to create a personalized learning experience for each individual student — essentially replicating the  role of a personal tutor.

Let’s break down what we mean by, “the role of a personal tutor.” There are four aspects to a personal tutor’s role:

1. To be aware of all the concepts within an area of learning and understand how they are linked
2. To identify which concepts a learner has already mastered
3. To construct an ordered learning path of the concepts the learner has yet to master
4. To support the learner as they attempt to master new concepts

For an adaptive learning system to be truly successful, each of these steps requires automating, so let’s think about what that might look like.

Firstly, let’s look at the knowledge of all the concepts within an area of learning, which we will refer to as a knowledge map. A knowledge map for an adaptive learning system must link all the concepts within a topic area and all the topic areas within a subject. Let’s use a very basic example to show just how complex this process is: to understand the number 5, a learner must understand its cardinality (that it can represent an amount e.g. five eggs), that it can be ordinal (the 5th item in a list) and that it can be nominal (referring to a particular object e.g. a player in a football team or a house number).

If all of this is built into understanding just a number, imagine how much knowledge is required to understand a complex mathematical concept like factorisation of a quadratic equation!

Once a knowledge map has been created, the next step in building a functioning adaptive learning system is to create a method by which the system can identify which concepts are already mastered and which are not.

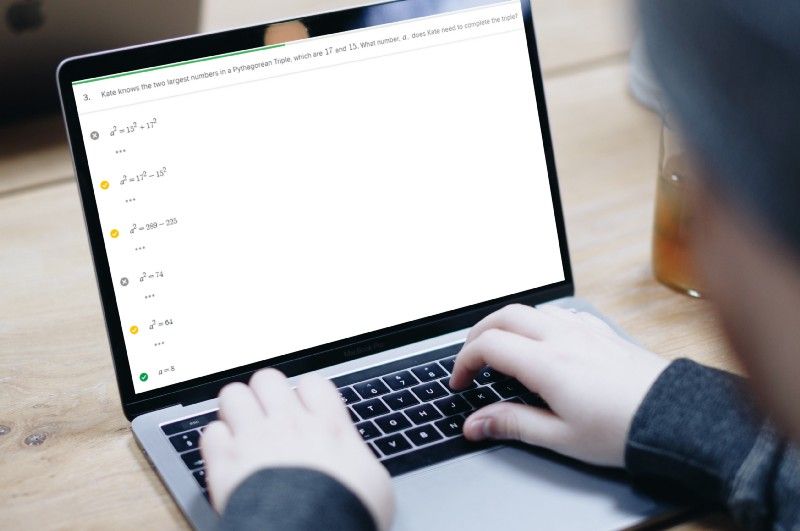
The way a teacher or tutor does this is to present the learner with questions and this is the logical method for an adaptive learning system to use too. However, the standard method for answering assessable questions on a computer is to use multiple choice as these questions can easily be coded as right or wrong. The problem with this method is that it misses out on all the steps and calculations that lead to a final answer and the learning that comes with all that working.

To really enable a learning program to identify what concepts the learner has mastered (and which they haven’t) the questions must be structured in a way that allows the learner to show their thought process, to enter their working. This process gives the learning program the ability to assess the learner’s knowledge and understanding. It also opens up more opportunities to provide feedback, and to help them master new concepts.

(We’ll talk a bit more about this in a minute!)

If this can be automated, then the third step is to automate the construction of an ordered learning path that helps the learner master the remaining concepts.

To  do this the system must combine the information it holds from both the knowledge map, and the data on the learner’s current level of understanding. It is then a simple process of closing gaps in an order  from most basic to most complex concept — an ordered learning path.

To clarify what we mean by an ordered learning path, we like to use the analogy of building a house. You can’t start decorating a house until it has a roof on it; you can’t put the roof of a house before building the  walls; you can’t build the walls of the house without first laying the foundations. Just as building a house must start with laying the foundations, complex mathematical concepts require you to first master all the simpler concepts on which they build.

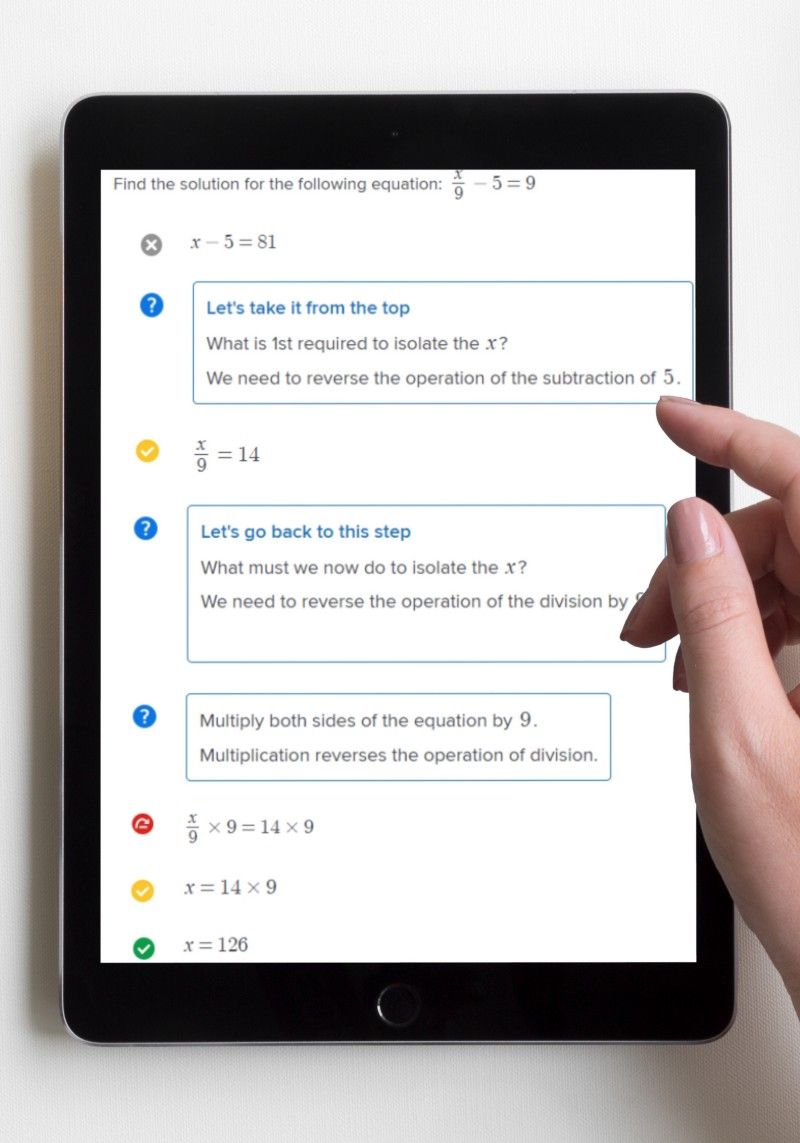
Once we have constructed an ordered learning path for the learner, we then need to help them to master new concepts. Clearly, mastering new  concepts requires more than just understanding any prerequisite concepts; it requires teaching of the new concept and practice applying the concept to consolidate understanding. Answering questions, even when showing working, is not enough. A personal tutor does not simply sit by whilst a learner practices, they monitor the learner, let them get stuck and puzzle it out when they can and intervene when required. Their intervention can be in the form of pointing out where a student has gone wrong, helping them understand what the next step might be or even showing them the next step. This is the final process that must be automated for an adaptive learning system to successfully replicate the role of a personal tutor.

Whilst  the other steps are challenging, it is this last step that is the most difficult. It requires an awful lot of work. Each and every question  relating to every reasonable concept must be considered and every method  of solving that question must be identified. Relevant question-level  feedback, such as hints and next steps, must be produced for all the  different ways a learner may use, so that when a learner gets stuck and requires help, the system can provide the most appropriate feedback.  With the advancement of artificial intelligence, no doubt this aspect of the process will also be automated in the future. But for now it still  requires a team of hard-working humans. (You can see how our team of  teachers at Mathspace achieves this in this video.)

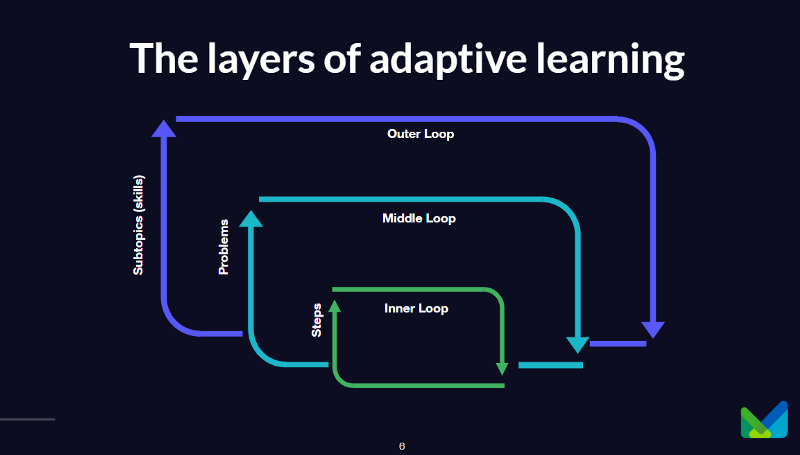
At Mathspace, we refer to this question-level feedback as the inner loop, it forms the first layer of the adaptive system, helping learners to solve  individual questions pertaining to a specific topic. In addition to this  inner loop, there is a middle and an outer loop. The middle loop  presents the next relevant question within  a concept to match the learner’s level of understanding — increasing or decreasing question complexity as a learner demonstrates understanding  or a lack of it. The overarching outer loop presents the next relevant concept based on the concepts already mastered — the personalised path through the knowledge map.

Adaptive learning is in its relative infancy as an educational tool, but the huge progress that Mathspace has made in the area shows the potential that technology can offer. No doubt adaptive learning technology will continue to advance and what’s possible in this space will continue to develop too. It’s certainly an exciting time to be working in education!