To infinity and beyond, with fractals

The Coffee + Math Series

We’ve squeezed in one final Coffee + Math catch up for 2017!

This week we defied the sweltering Summer heat and had a hot chocolate with Adam Humphreys in Sydney, Australia.

Before  joining Mathspace, Adam was entrenched in the world of academia,  devoting half his time to math, and the other half to physics. He now  spends his days crafting the math questions that you find on Mathspace.

Coffee of choice?

Hmm…. I’m not much of a coffee drinker — I prefer hot chocolate.

Have you heard of this saying?

Mathematicians are machines for turning coffee into theorems.

At least I know why there aren’t any theorems named after me yet!

Favorite math equation/fact/field of study?

There  are far too many interesting areas of mathematics for me to pick a  favorite! There is one area that I’m particularly interested in. It’s  the wonderfully infinite, self-replicating world of fractals.

Ok… And what exactly is a fractal?

A fractal is an object which looks more or less the same at any scale. This means  that no matter how much you zoom into a fractal, the detail looks  pretty much identical.

Can you give us an example?

I knew this question was coming, so I’ve drawn some!

This one is called Sierpinski’s Triangle…

This one is called the Dragon curve…

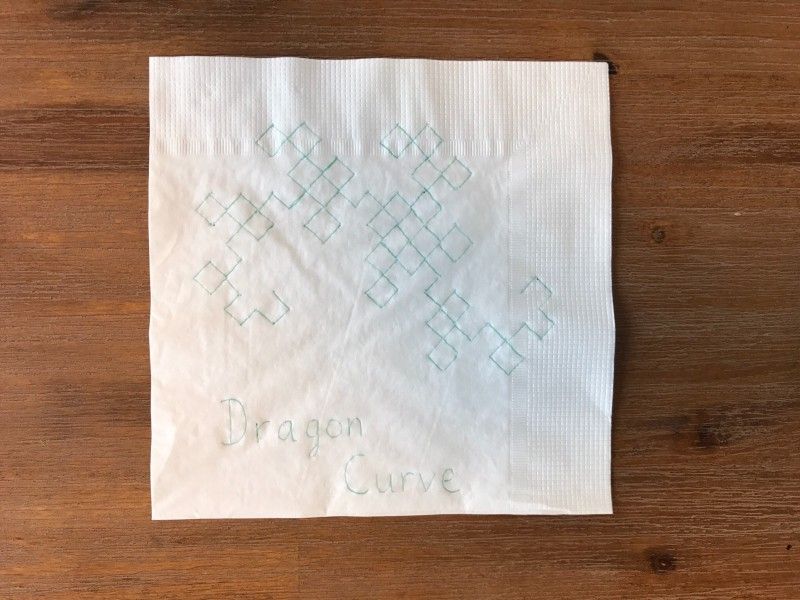
And this one is called the Koch curve…

I will point out that these are approximations. It’s actually quite tricky to draw fractals on serviettes and, believe it or not, I cannot draw to an infinitesimal scale!

All of these fractals are what’s known as self-similar fractals, which means that their detail is exactly identical as you zoom in.

This means that you can find exact copies of the fractal, inside of itself.

Can you tell us more?

One  thing I love about fractals is that they are so visual. Some fractal  patterns (like the examples above) are great to scribble because they  can be constructed by following an iterative process.

In  general, self-similar fractals can be constructed from some “base  piece” by arranging copies of the base piece in a particular pattern,  then shrinking that pattern to use as your new “base piece” and  repeating. (The process can also be done without shrinking, which is  easier to draw but takes up an increasingly large amount of space).

Here are a couple of iterations of the above curves drawn in this way:

Of  course, any such construction can only go for so many iterations before  you run out of space, so the physical representation is only an  approximation of the true fractal.

If we take the mathematical concept all the way to the infinitesimal, however, things start to get a little, umm, weird.

Weird? How exactly?

Any  time infinity dips its toes into an area of mathematics, you can expect  there to be something that doesn’t fully match your intuition.

What if I told you that fractals don’t conform to our usual notion of dimension?

For  conventional shapes, we can think about dimension by measuring an  object with a certain unit of measurement, then remeasure using a  smaller unit of measurement and seeing how many more pieces you get.

For  example, here I’ve drawn a line, a square and a cube of 1 “unit” side  length, and then remeasured them using a unit that is ⅓ of the size. For  the line there are now 3 = 3¹ pieces, for the square there are 9 = 3²  pieces, and for the cube there are 27 = 3³ pieces.

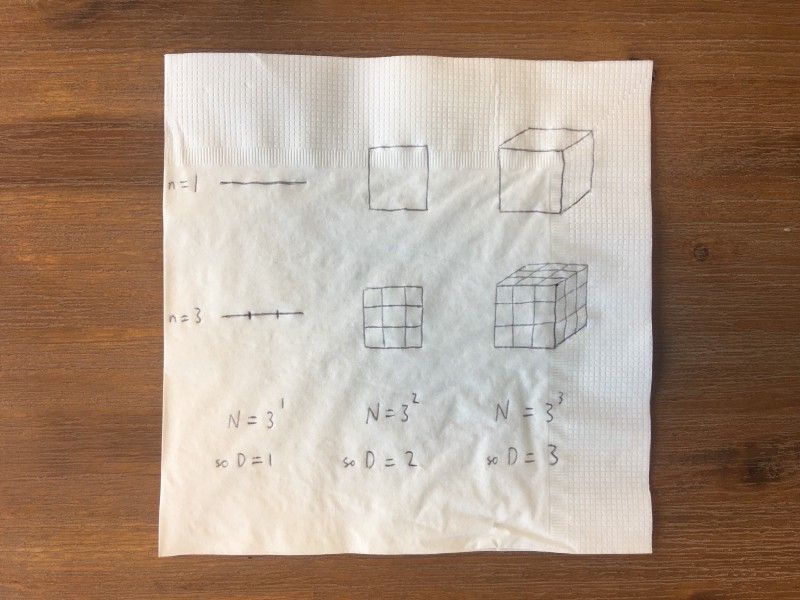
In  general, if we use a unit of measurement that is 1/n times the size and  get N pieces, then the dimension D of the object satisfies N = n^D. (So  the line has n¹ pieces, the square has n² pieces, and the cube has n³  pieces). Rearranging, we get that D = ln(N)/ln(n). So far so good.

Now  let’s take a look at the Koch curve. You would be forgiven for thinking  that the Koch curve is 1 dimensional — after all, each step of the  iterative construction that we used earlier is just putting straight  lines together. But this is where infinity steps in and shakes up our  intuition: when we iterate the process to the infinitesimal, there  aren’t really any “straight line pieces” left anywhere. Instead recall  that at each step of of the construction we took 4 pieces that were ⅓  the size, and repeat this to the infinitesimal. So we have that the fractal dimension of the Koch curve is D = ln(4)/ln(3) ≈1.262 — which is not a whole  number! This indicates that the Koch fractal is somehow more than just a  line, with its infiniteness kind of “pushing out” into more than one  dimension.

In  a similar way, when we constructed Sierpinski’s Triangle we used 3  copies of lines that were ½ the size. So for Sierpinski’s Triangle we  have D = ln(3)/ln(2) ≈1.585. This number is larger than for the Koch  curve, and we can see this difference visually — Sierpinski’s Triangle  fills up much more space than the Koch curve.

There’s more, let me….

(At this point I cut Adam off. I try to ask another question, but he won’t stop talking….. )

Let  me now show you another type of fractal curve, known as the Hilbert  curve, which was discovered in 1891 by the mathematician David Hilbert.  The first few steps of its construction look like this:

You  might notice that this curve seems to be winding around in such a way  that is filling up a lot of the space — even more than Sierpinski’s  triangle, which had obvious regions of holes.

Well, what is the fractal dimension of the Hilbert curve?

At  each step we are using 4 pieces that are ½ the size (and a little extra  line to join the pieces). So we have that D = ln(4)/ln(2) = 2. That is,  when taken to the infinitesimal, the Hilbert curve is actually two  dimensional, despite being constructed from straight line pieces!  Indeed, when the fractal is taken to the infinitesimal it is  indistinguishable from a solid square, and curves such as this are known  as space-filling curves.

Our  friend the Dragon curve is also a space-filling curve, although it  fills space in a less straight-forward way than the neat square of the  Hilbert curve. Once again, we can see this by looking at the fractal  dimension of the Dragon curve. At each step we use 2 pieces that are  1/√2 times the size (or alternatively, every second step uses 4 pieces  that are ½ the size), and so we have that D = ln(2)/ln(√2) = 2.

Why do you think fractals are so important?

I  don’t think they are “important”, per se, but there are a number of  naturally occurring structures that have a fractal-like nature. Of  course, anything in the physical world has a limitation on its detail as  you get to an atomic scale (this is something funny showing you what I mean). So they will only be approximations of true mathematical fractals.

The most obvious of these are snowflakes, which have a fractal-like crystalline structure.

Lightning strikes are another natural phenomena which often display a fractal nature as  the bolt spreads out from the cloud, searching for the best point of  contact with the ground. This is one of the best slow mo videos I’ve seen which shows the beauty of lightning fractals.

There are also nutritious fractals! Romanesco broccoli is a great example of an edible (and healthy) fractal.

Anything else interesting to add?

Yes, actually.

Earlier  I talked about an iterative method of generating self-similar fractals.  You might recall that we constructed the Dragon curve by placing two  copies of the previous iteration at right angles to each other, starting  from a straight line. It turns out that this is exactly what you get if  you fold a sheet of paper in half repeatedly (folding in the same  direction) and then unfold it so that each fold is a right angle!

So you can get origami fractal approximations too.

Oh, and fractal patterns also make for awesome desktop backgrounds! (Try a quick image search for “fractal wallpaper”).

We’d be keen to know of any other unusual methods to generate fractals. Please share below!

Keen to read more from the Coffee + Math series? Check out our last post in which we explore the intersection of math and poetry, with Euler’s Identity.