The Mathematical Reason for Deuce

and other intriguing insights into the world of tennis scores

Last Monday morning at Mathspace HQ we started the day with an impassioned debate. It was about the first Grand Slam for 2018 — the Australian Open.
What initially started as a chat about the Kyrgios/Dimitrov duel that had unfolded the night prior, ended in a more general debate about the origins of the unique (and, let’s be honest, weird) tennis scoring system.
Love, 15, 30, 40, deuce, advantage….
What does it all mean? And can we think about any of this mathematically?
It all starts with love (or l’oeuf)

In tennis, if you’ve scored no points, your score isn’t zero. It’s love.
‘Love’ originally comes from the French word ‘l’oeuf,’ meaning egg. An egg looks like a zero.
Somehow, over time, English speakers turned “l’oeuf” into “love”. And it stuck.
15, 30, 40…

If you win a point your score isn’t ‘one’. Instead, your score goes up to 15, and then 30. But after 30 it goes to 40, instead of 45 (as you’d expect).
Now the jury is out on the reason for this one, but there are a few possibilities.
My personal favorite is that early in the game’s history you only needed four points to win a game, and scores were marked on a clock. So you would start at 0 for the beginning of an hour and then go up 15 minutes, 30 minutes, 45 minutes and 60 minutes which is the end of the hour.
But these aren’t quite the scores today. So what happened?
It’s possible that 45 was changed to 40 just because it’s easier to say in French. But that would be too boring. I prefer to think that it was changed to 40 to make space for a new score when the deuce rule was introduced.
Deuce was introduced to reduce the impact of the lucky shot…
Deuce
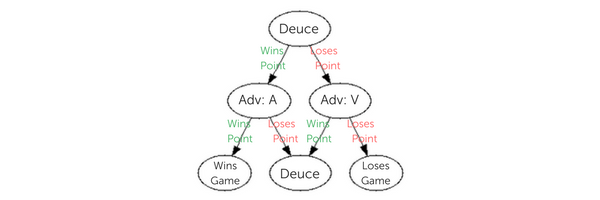
If both players get to 40, the score becomes deuce. At this point, if you win a point you get to advantage, and you need to win another point to win the game. If you lose a point when you are on advantage, the score goes back to deuce. Deuce effectively means you need 2 points in a row to win the game. So I’d say that Advantage is 50 and Game is 60 on our clock point scoring system.
But why introduce ‘deuce’ in the first place? There is a mathematical answer!
The short answer is that deuce makes tennis fairer.
Let’s assume that each player has a constant chance of winning any point. Suppose we have two players, Amis and Vauquelin. Amis is a stronger player, and so has a 70% chance of winning each point. Vauquelin consequently has a 30% chance to win a point.
Without the deuce rule, if both players get to 40, Amis has a 70% chance to win the game on the next point and Vauquelin has a 30% chance.
With the deuce rule, if both players get to 40, then they would need to win two consecutive points to win the game, since if they each won one point they would go back to deuce. So the probability of winning the game at this point is the probability of winning one point, squared. For Amis this becomes 49% and for Vauquelin this becomes 9%.
The remaining 42% is the probability that the score returns to deuce. Since each deuce is effectively the same situation, we can find the probabilities of winning after any number of deuces by dividing each of the probabilities above by the probability of either player winning. This gives Amis approximately 84% chance to win, and Vauquelin approximately 16%.
This is quite a dramatic change from 70% and 30% respectively. The stronger player has an even greater chance to win than their initial probability would indicate making for a fairer match by reducing the element of luck and rewarding the actual stronger player. And this reason extends to all the scoring rules in tennis.
While the calculations are a little complicated for this blog post, we can even work out the probabilities of winning from the start of a game. Without the deuce rule, Amis has a probability of around 87% and Vauquelin has a probability of around 13%. With the deuce rule, Amis has a probability of around 90% and Vauquelin has a probability of around 10%.
It’s worth noting that all of these numbers are based off a fairly simplistic assumption. The probabilities are more likely to change with each point. For example, some players are stronger when serving and others are stronger when receiving. That said, there’s an entire branch of mathematics called stochastics which answers questions like this.
Fun fact
The longest single game of tennis had 37 deuces! Assuming each player had a 50:50 chance of winning each point this was approximately a 1 in (1.9 x 10²³) chance of happening.
Thanks to our resident mathematician (and now, tennis expert), David Groenhout, for this post!

