Stones and apples

A thought experiment

Consider, far out in the depths of space, two identical objects, alone but for each the other’s twin. Let’s call one of them Alice and the other Bob, as is the tradition in thought experiments.

To complete the setup, we note that Alice and Bob are both spherically symmetric, that they have the same mass, that there is no net charge which would lead to any kind of electrostatic attraction, and that they are initially at rest with respect to each other. This is, more or less, the simplest thought experiment we could possibly imagine: a couple of stones sitting still some distance apart.

Now we ask the obvious question. If we keep watching Alice and Bob, what do we see? It turns out that, regardless of their mass or the distance separating their initial positions, what we would observe is that Alice and Bob begin to move toward each other. Ever so slowly at first, then quicker and quicker. They will be seen to accelerate towards one another until they ultimately collide.

This is no trick question, and you may be thinking that the observed behavior is entirely what we would expect. Maybe so, but suspend your intuitions for a moment and reflect on just how strange this situation actually is. Place Alice and Bob in an empty universe and they will eventually find each other. Without even looking, they come together — not by doing, but simply by being.

What is going on here? Recall Newton’s first law of motion:

Stuff that isn’t moving will keep on not moving, and stuff that moves uniformly will keep on moving uniformly, unless you force it to move differently.

That is, objects at rest can only start moving (and objects moving in a straight line at a constant speed can only change direction or speed) under the action of some force.

The way an object moves in response to a force is described by Newton’s second law of motion, F = ma. Given the force, we determine the acceleration. So, having observed the acceleration of Alice and Bob, can we infer a force?

A model of motion

To help us visualize the motion we are dealing with in this thought experiment, let’s draw a diagram that shows the position of an object at different points in time. A third object, which we’ll call Charlie, will join us for this part of the experiment.

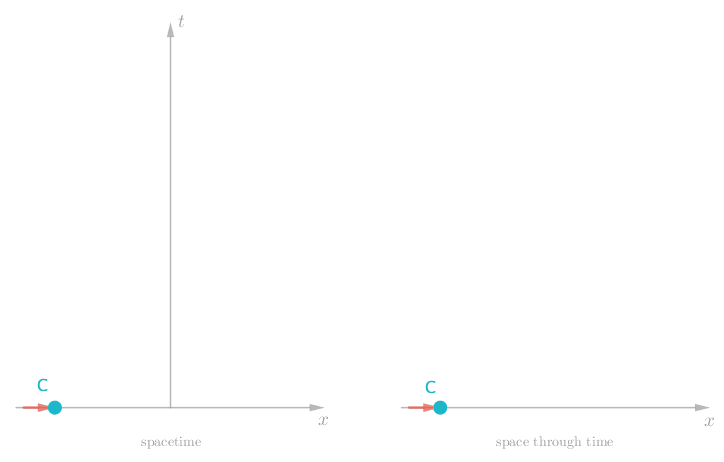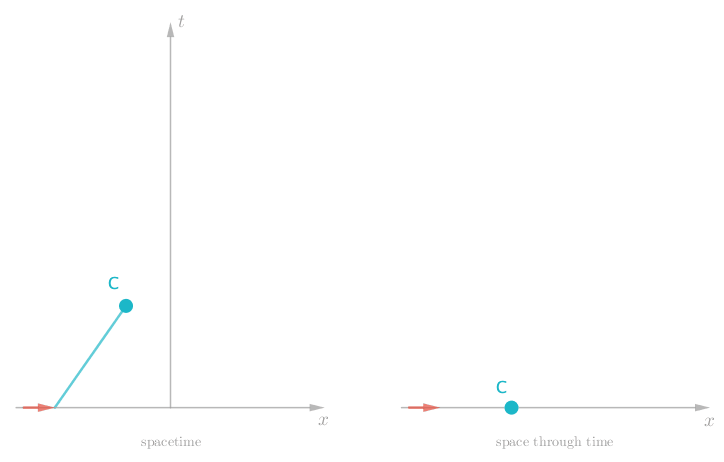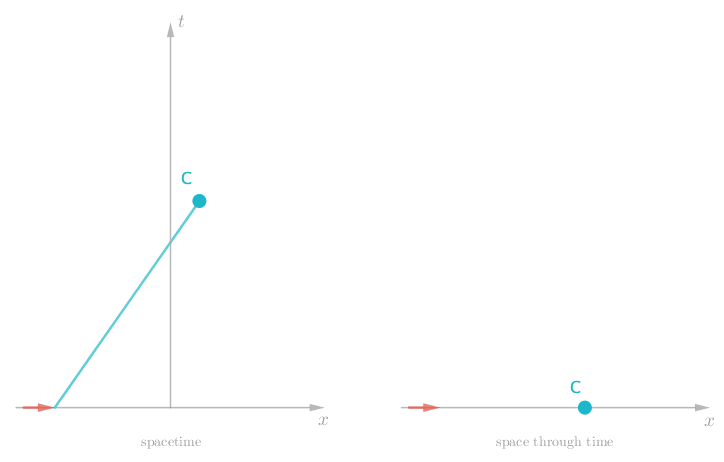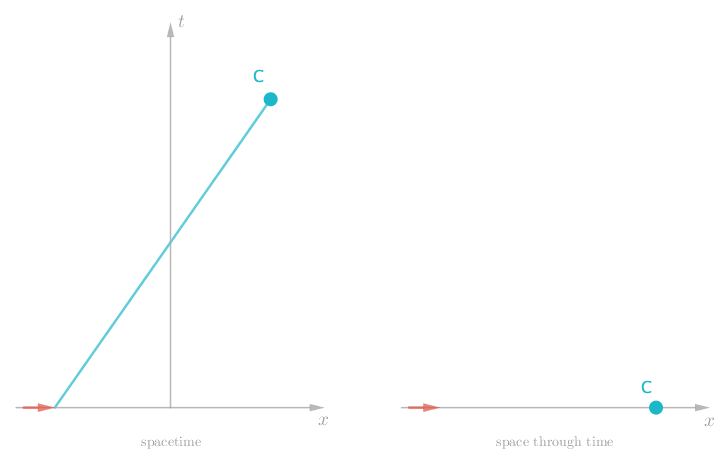
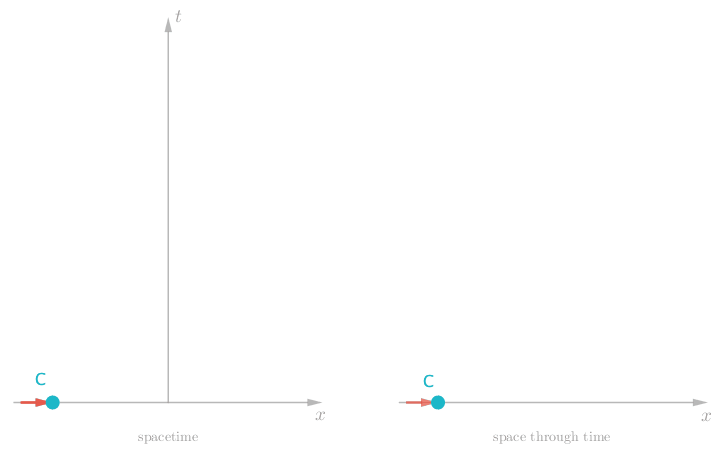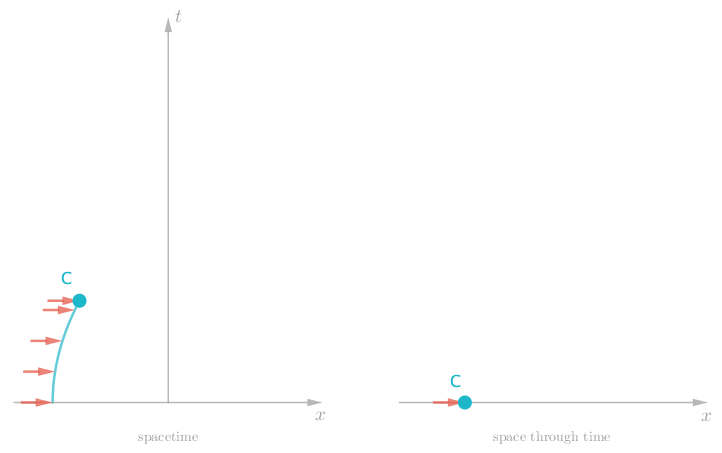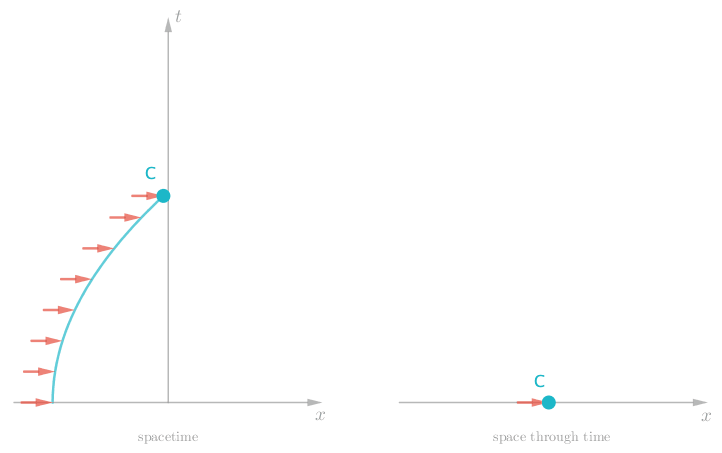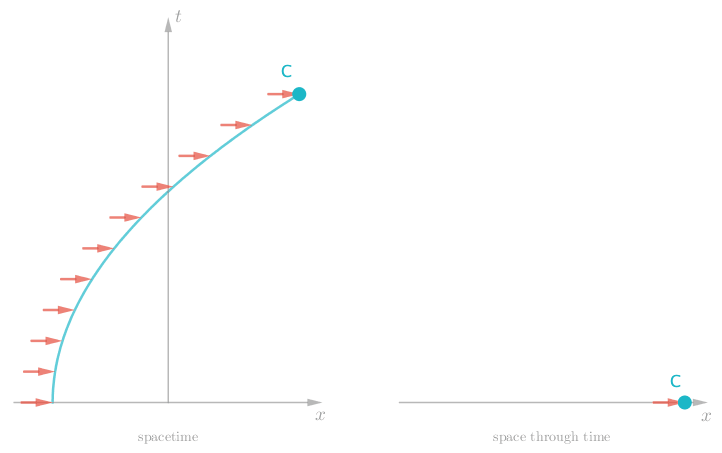
If Charlie is initially at rest, and is acted upon by no forces, we observe the very unexciting timeline shown below.

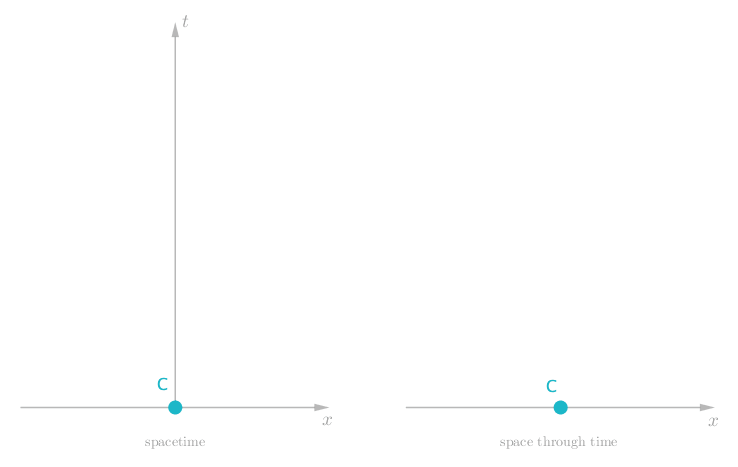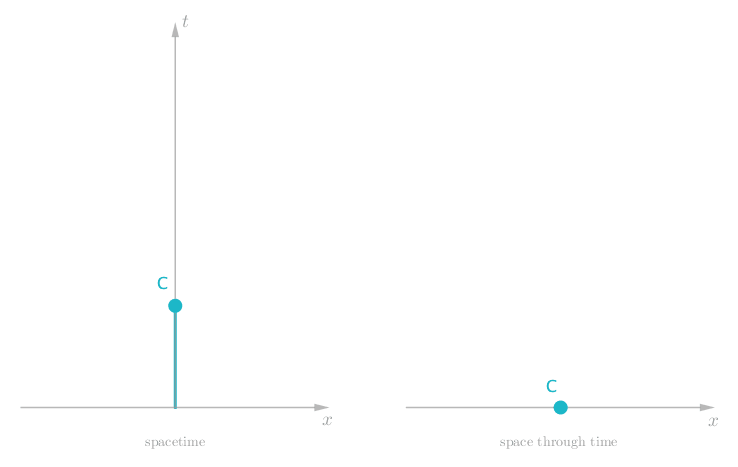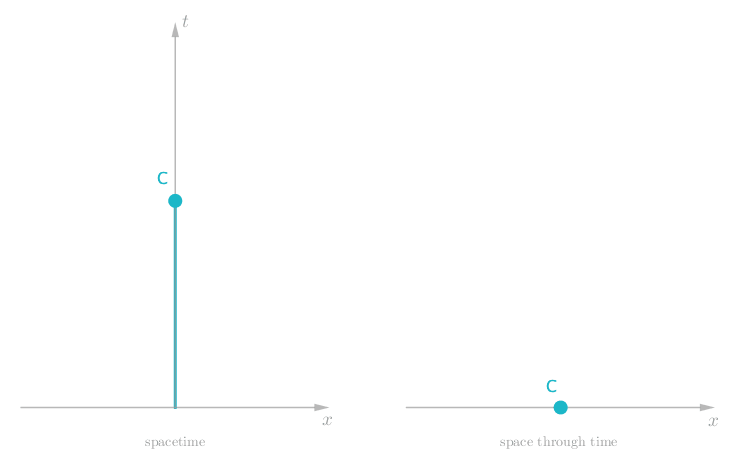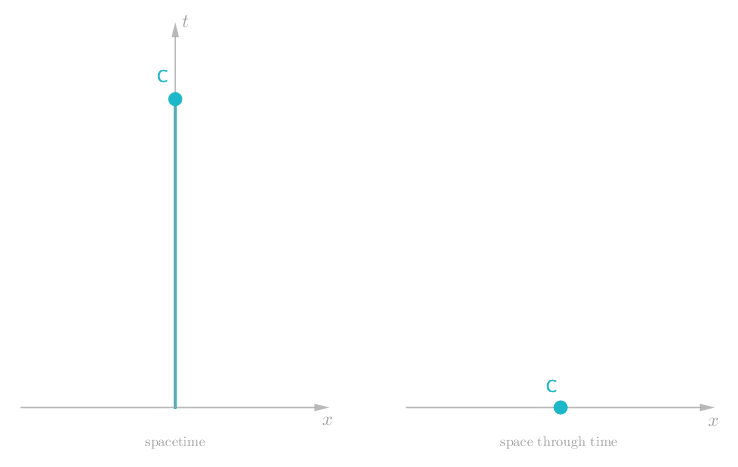
Pretty tame, but what more would we expect from a single stone out in deep space? Well let’s give Charlie a big shove to boost his speed. Now we see Charlie move off in one direction at a constant rate, since there is nothing else out there in deep space to slow him down. Charlie’s timeline is now more sloped.

So it looks like forces make for more interesting timelines. What if we apply a constant force, by strapping Charlie to a rocket? We would get a constant change in speed — an acceleration.

As a final example, we can see the effect of a dynamic force, where even the acceleration Charlie experiences is constantly changing. Attach Charlie to a spring and we observe him bounce back and forth.

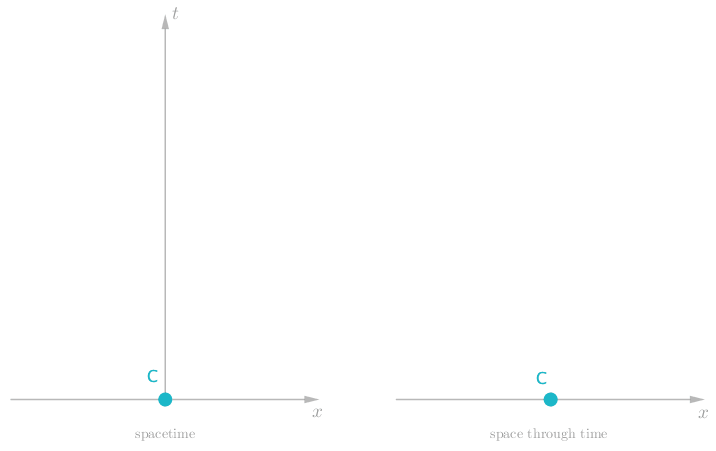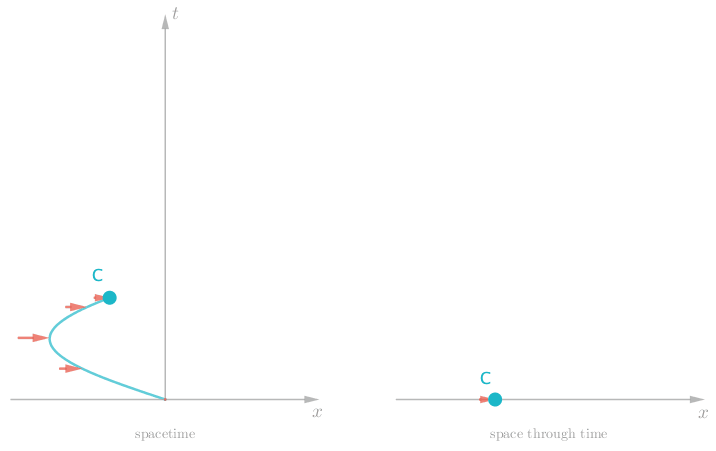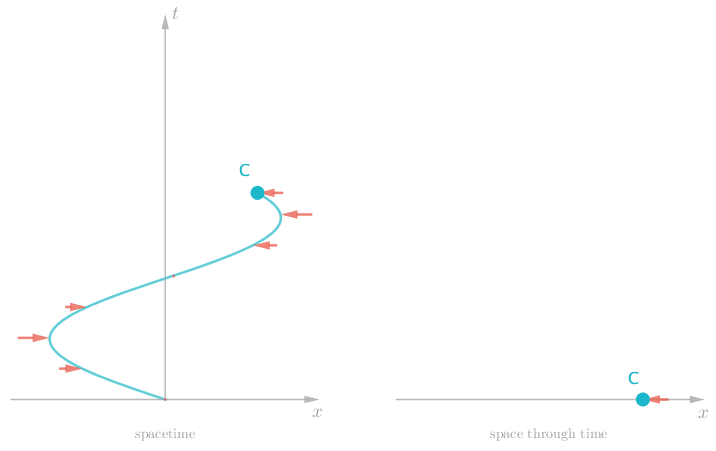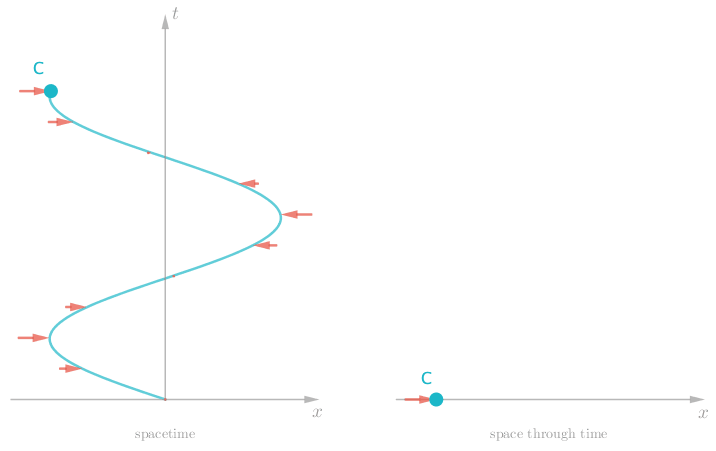
Now that we are experts with this type of visualization technique, we can introduce some formal terms for the things we have been talking about. A diagram that has a space axis and a time axis is called a spacetime diagram. The path of an object through a spacetime diagram is called a worldline.

Spacetime diagrams are really very simple, but they have some interesting features. You may have noticed that Charlie was always moving through spacetime, whether or not there were any forces pushing or pulling him around in space. Even when Charlie was initially at rest (in space) we saw that he was moving consistently through spacetime. Most notably, when no forces are present we see Charlie move along a straight worldline (as in figure 3 and figure 4).

If we do away with thinking of motion in terms of space and time, and we fully absorb the implications of spacetime thinking, then it becomes apparent that being at rest is no longer a meaningful concept. How can something stand still in space and time? Further, it can be shown (through more sophisticated treatments than are worthwhile here) that when forces are present, they only ever act to change the direction of an object’s worldline, never the speed of that object through spacetime.

We can summarize these ideas in what I’ll call Einstein’s first law of motion (which you should compare to Newton’s first law above):

There is no stuff that isn’t moving. Stuff travels at a constant speed, and will move along a straight worldline unless you force it to move along a curvy worldline.

Now you may be wondering, if everything is moving at the same speed through spacetime, what speed is that? Unfortunately this also requires a treatment outside the scope of this article. But suffice it to say that Einstein’s law is a universal law applied to all objects, and the universe itself has a “speed limit” - the speed of light. So if everything is moving at the same speed, what other speed could it be, other than the speed of light?

Putting the model to work

With all this in mind, let’s now return to our original scenario with Alice and Bob. What we want to do is to be able to describe the situation we observe in space and time (in figure 2) on some kind of spacetime diagram. Starting with Einstein’s law of motion, we have two possible paths to arrive at a satisfying description; we can use forces, or we can make do without them.

The first path is easy. Suppose that there is an attractive force between Alice and Bob, analogous to the electric force between two oppositely charged particles. We see Alice and Bob accelerate, so we know that their worldlines through spacetime will be curved. This suggests that the force acts continuously. The spacetime diagram for this case is shown below.

There is a robust understanding of how electrically charged objects interact under the influence of electric forces, so it is not too far fetched to think that “mass charged” objects like Alice and Bob can be influenced by “massive” forces. Nevertheless, uncovering the exact nature of this massive force will be a considerable challenge. So it is worth our efforts to see if we can find a way to describe the motion of Alice and Bob without calling upon any forces.

We are now on the second path, and though we proceed confidently we are quickly met by significant obstacle. If there are no forces acting on Alice and Bob, then both their worldlines will be perfectly straight. In particular, since they are initially at rest in space, their worldlines will be initially parallel, and will stay parallel as they both move through spacetime.

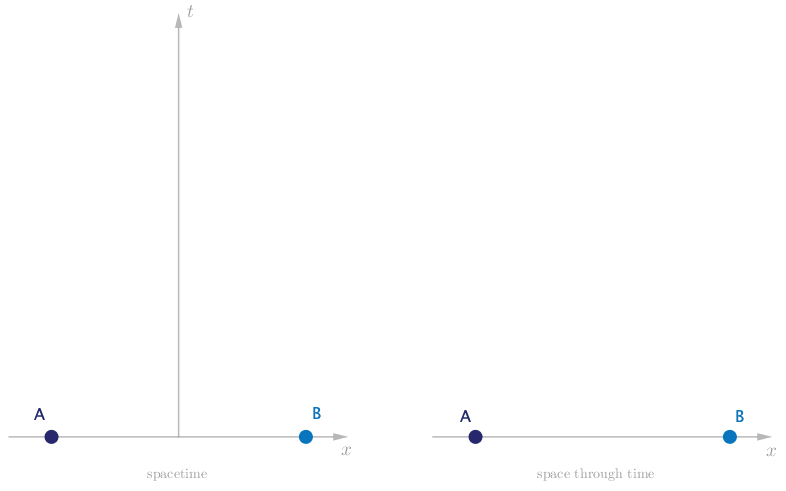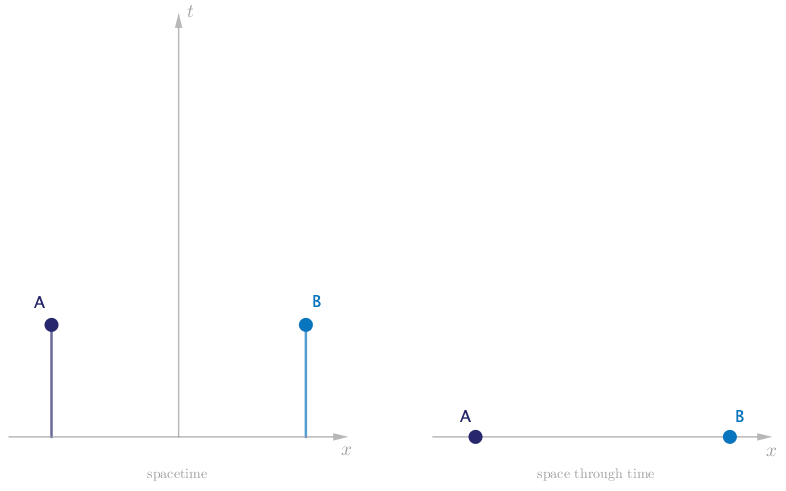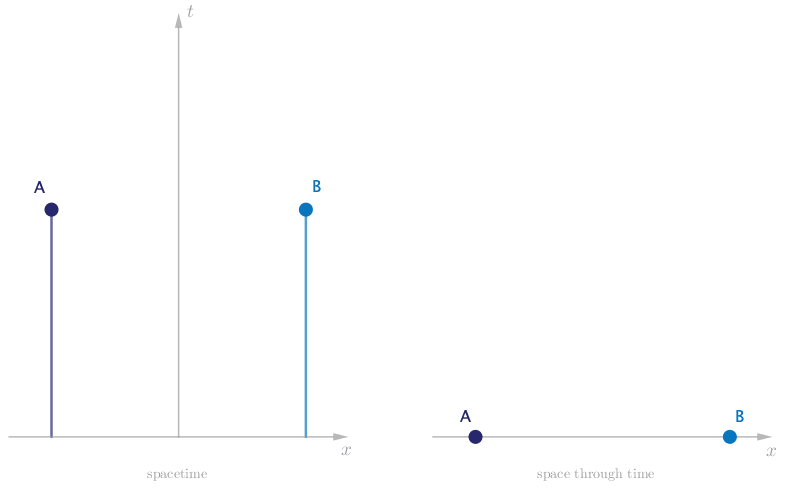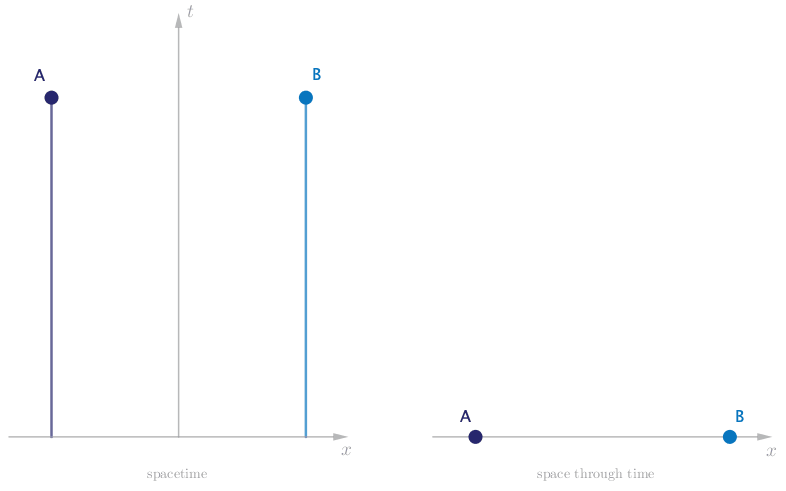
How can it be that two objects, initially traveling in parallel, can continue each moving in a straight line and yet end up meeting one another?

If you try sketching out a few worldlines on paper, you will soon find that it is very difficult to make Alice and Bob collide. Which is not too surprising, since in fact it is impossible to draw on paper two parallel lines that meet at a point. Paper, tabletop, door, wall or floor – try any flat surface and the result will be the same. In some sense it is the definition of flat space that parallel lines do not intersect.

Lines and curves

Luckily for us the world is also full of lots of very unflat things. Why not try drawing a spacetime diagram on a curved surface? An apple seems like an appropriate choice.

Imagine Ash and Bernhard are two ants exploring the surface of an apple. We encounter them both standing at different points along the apple’s equator, both facing the apple’s stem. As they begin to walk stemward we notice that their paths are initially parallel. Being very rational and economic ants, Ash and Bernhard are each following the shortest possible path from their respective starting positions on the equator of the apple, up to their common goal of the stem.

By taking the shortest possible path, both ants walk in what is essentially a straight line along the curved surface of the apple. If calling it a straight line seems a bit odd, just think about what a straight line in flat space represents; it is the shortest possible path between two points. It’s just that Ash and Bernhard are confined to the apple’s surface, they can’t dig down and chew their way through the middle of the apple. Their path is straight, it is only the space they travel through (the surface of the apple) that is curved.

And so we see Ash and Bernhard, initially traveling in parallel, can continue each moving in a straight line and yet end up meeting one another. The big idea here is that their paths were allowed to eventually intersect solely due to the curvature of the surface of the apple, not because of any force pushing or pulling them away onto anything other than the shortest possible path to the stem.

Circling back

Are we not now ever so close to our solution? Have you made the connection already? Of course Alice and Bob could never meet traveling along straight, parallel worldlines in flat spacetime. But just as Ash and Bernhard “collided” because they were walking along a curved surface, so too can Alice and Bob collide if they are moving through a curved spacetime!

Finally we are able to draw a spacetime diagram that faithfully describes the motion we observe, and with not a force in sight.

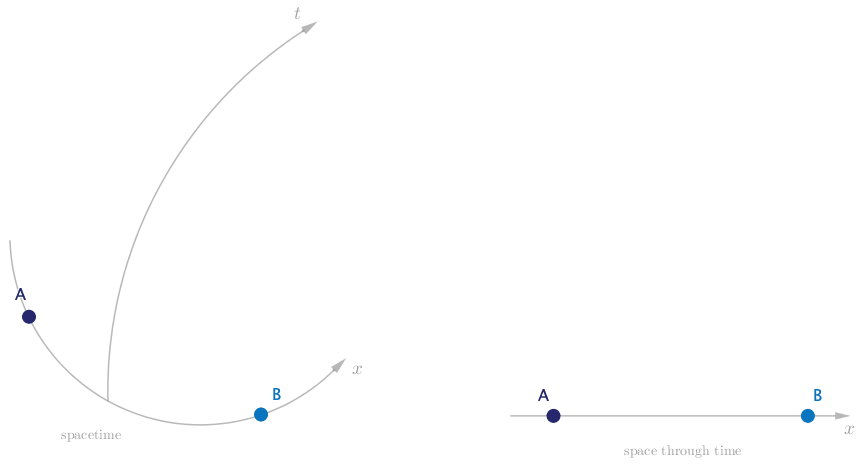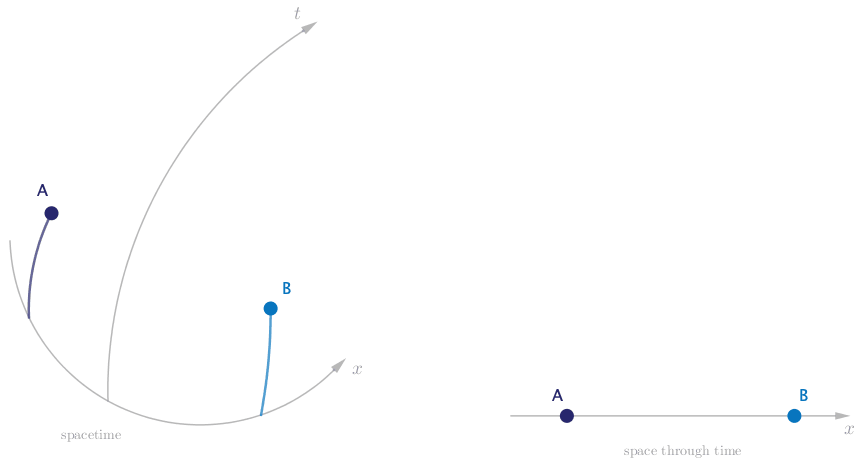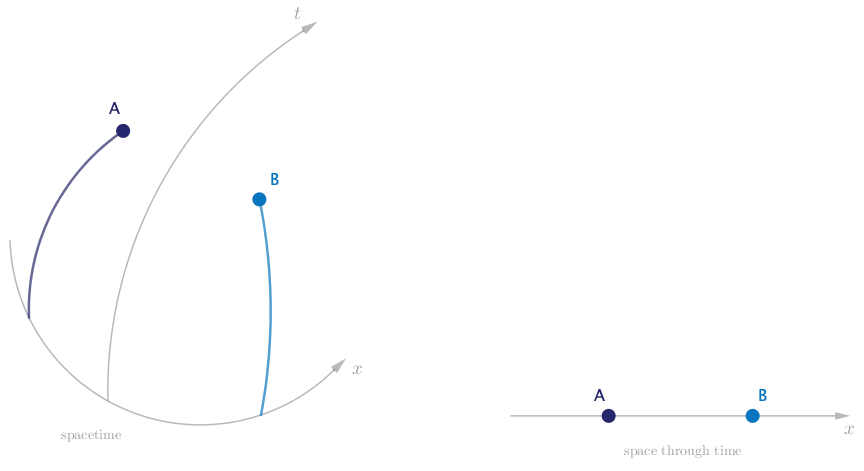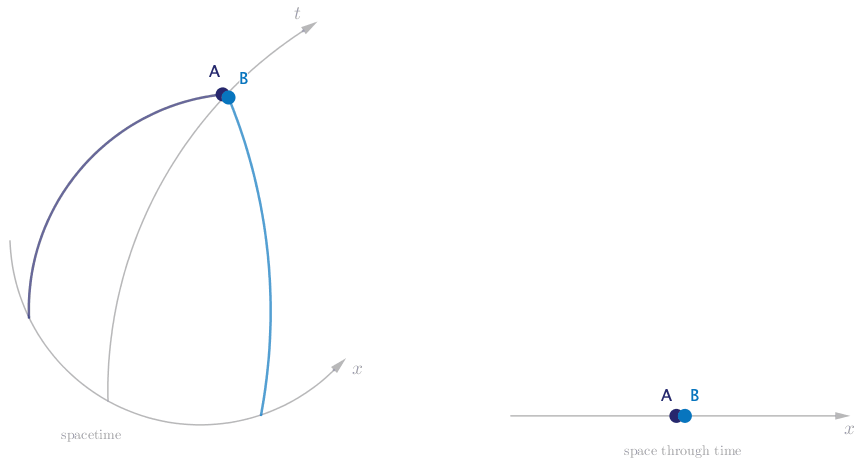
Let’s double check that this description is consistent with Einstein’s law of motion. Alice and Bob move at a constant speed through spacetime, and since there are no forces present, they move along straight worldlines. But since the spacetime is curved, they end up accelerating toward each other and eventually colliding.

Apples and stones in freefall

People all over the world have been thinking about gravity for a long time, and although we have made substantial progress, there are still many things about the nature of gravitation that we do not fully understand. Some of the most profound insights came from the work of Isaac Newton in the 1600s, then later from the work of Albert Einstein in the early 20th century.

Newton conceived of gravity as an attractive force acting between all masses. Celestial bodies and earthly ones are all governed by those same laws of motion. Many of his ideas were so groundbreaking that they couldn’t be described by any of the mathematics that existed at the time. Newton had to invent calculus himself just so he could formalize his theories.

Einstein reimagine gravitation not as the action of any force, but as the coupled interaction of mass and spacetime: masses cause spacetime to curve, and in turn spacetime governs the way masses move. Einstein had very capable mathematical abilities, but his real talent was his highly creative imagination.

He also famously loved thought experiments. It is appropriate now to compare side by side the results of our exploration of the motion of Alice and Bob, first from the perspective of Newton gravity, then from the perspective of Einstein gravity.

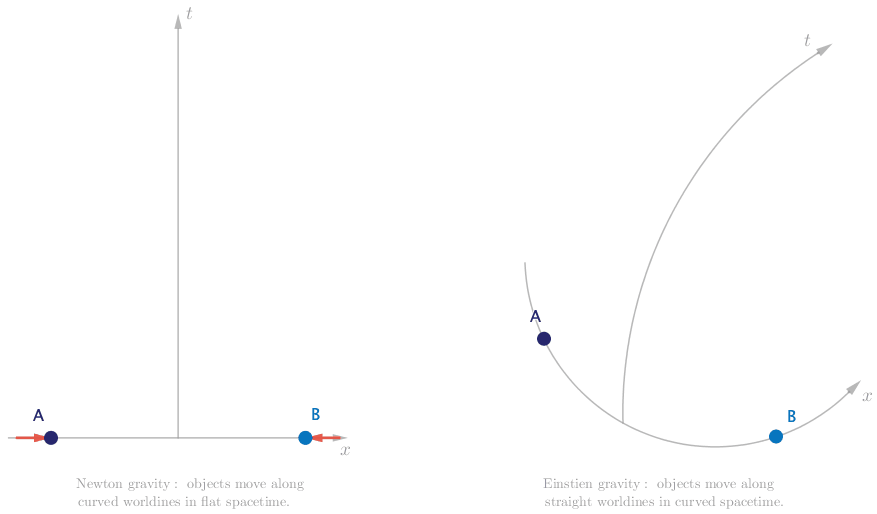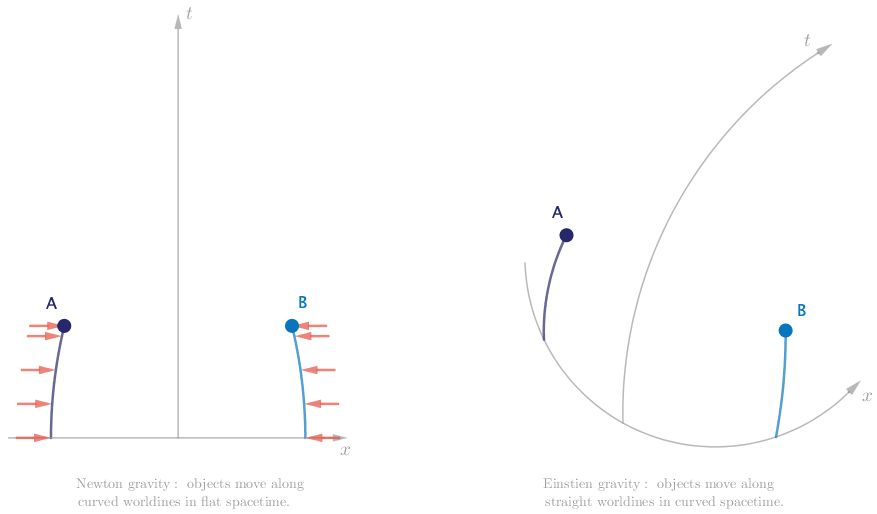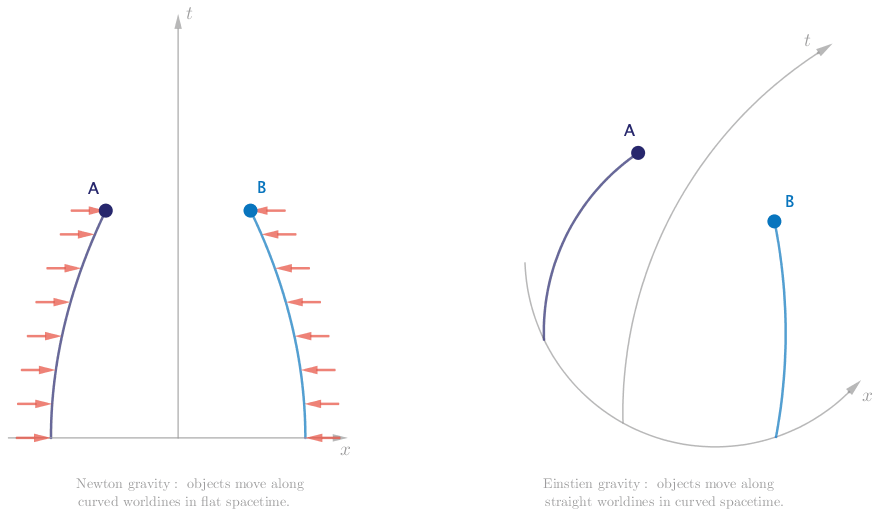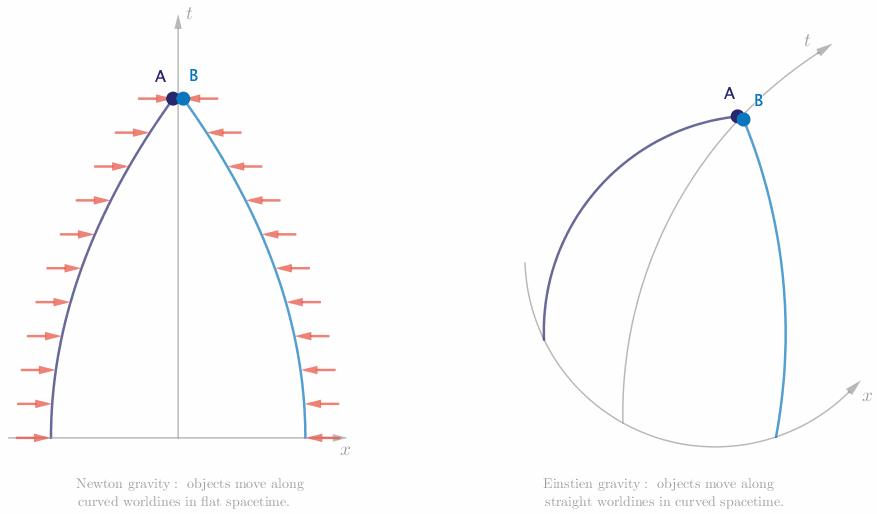
While Einstein’s is considered the more accurate theory of gravity, there are many situations for which Newton’s approach is good enough. Which would you use to describe the way an apple hangs on a tree, and the way it falls? Which would you use to describe a long distance flight? What about the orbit of satellites around the Earth, or the Earth around the Sun? Which would you use to describe the image of a distant star as it is eclipsed by a black hole?

After all the successes of these theories, there are still phenomena we observe in our world which are not explained by Newton gravity or Einstein gravity. For these we need a better theory, and this will almost certainly require much more creative and unorthodox thinking to develop.