Mixed Numbers: An Educator’s Guide

In many countries mixed numbers are introduced in middle primary. But why? And what use are they?

Why and where?
Whether you teach in Australia, the United States, Canada, New Zealand, United Kingdom, Hong Kong or Singapore; mixed numbers are introduced in middle primary. But why? And what use are they?
Those familiar with more senior mathematics would know that we rarely use mixed numbers in those settings, so why include mixed numbers in the junior curriculum?
The detail that each curriculum authority provides about mixed numbers is usually sparse.
For example in Australia, mixed numbers are mentioned in Year 4, here is the only mention of mixed numbers in all of primary school fractional

In the Common Core in the United States, it is only mentioned through one of the examples provided for 4.NF.3b.

Singapore details the most, in Primary Year 4 it lists 5 dot points about how to relate mixed numbers and improper fractions together.

How I interpret this, is not that mixed numbers are being considered unimportant, but instead that they actually interconnect with broader fraction work, utilising both representations of mixed numbers and improper fractions where it makes sense to do so. Hence developing the number sense surrounding mixed numbers throughout fractional development.
The conceptual process for developing understanding of mixed numbers
Having worked with programs focussed on the development of deep understanding of fractions for over a decade, I have come to see that the following presents as a good foundation for mixed numbers.
- Develop the idea of a mixed number as being another representation of the improper equivalent. This can be developed through the use of diagrams and manipulatives.
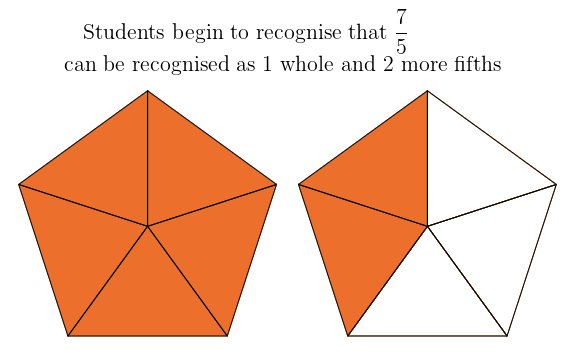
Formal conversion rules, such as multiplying and adding should not be taught in the introduction, but students should be allowed to develop this understanding through playing with the manipulatives, conversation and explanation of their thinking.
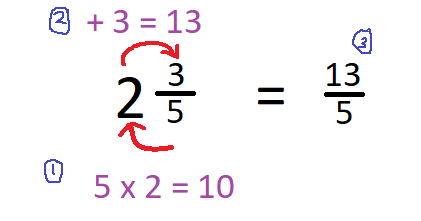
2. Plot and identify the size of mixed numbers on numbers lines, or with other physical representations

3. Order and count with mixed numbers. Counting both using mixed numbers,
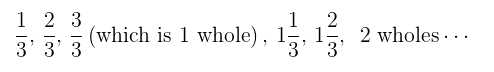
and with improper fractions,
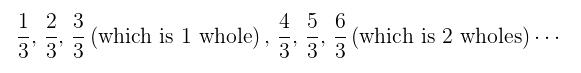
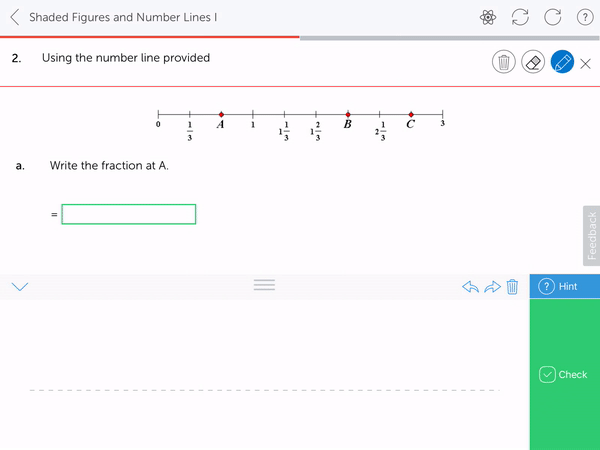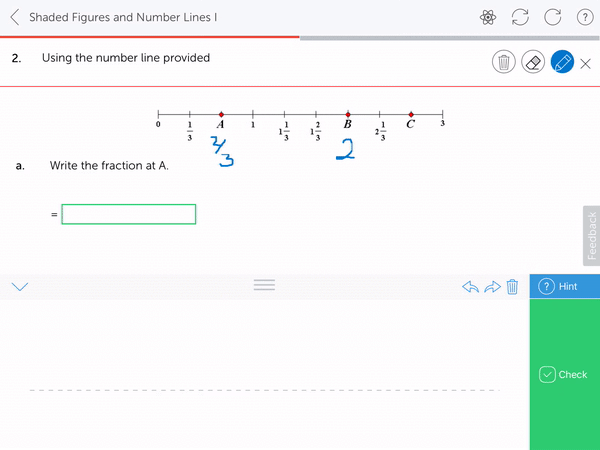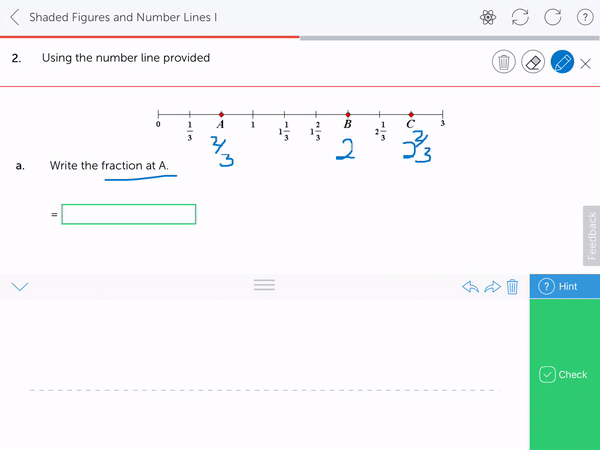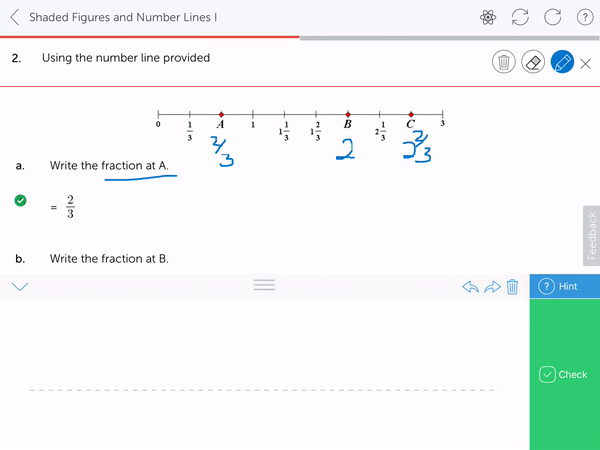
4. Reason and understand the mixed number representation from an improper fraction, for example that 6 fifths is 1 wholes (5 fifths) and 1 more fifth. Not by way of conversion, but by way of understanding. Use of pictorial representations is essential here.
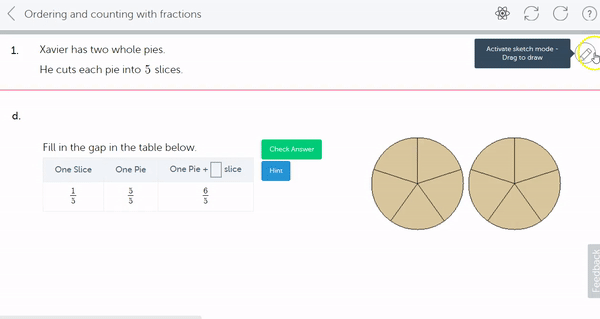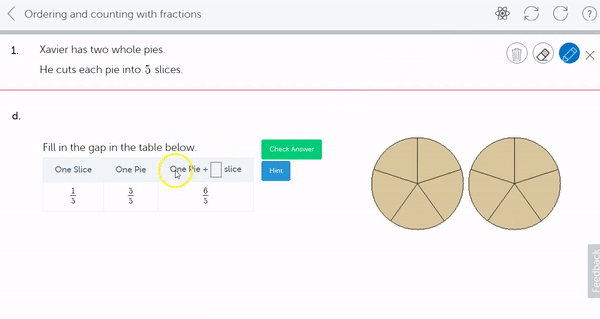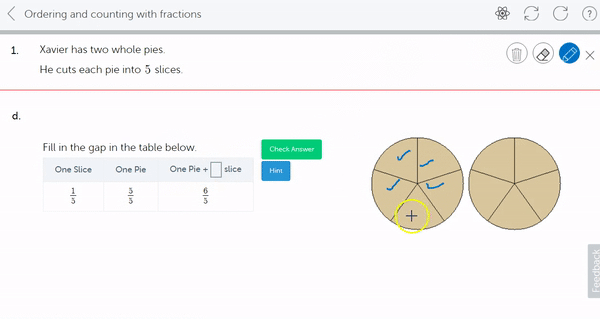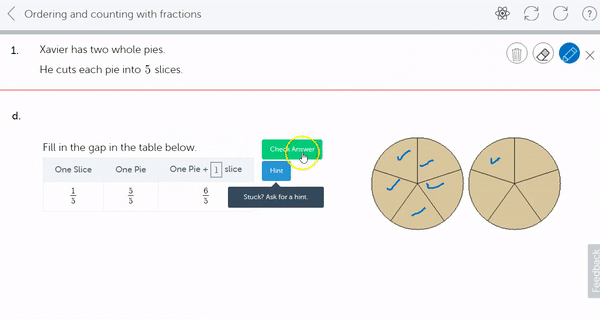
5. Benchmarking, (or rounding) mixed numbers, to common values like 0, ½, 1, or any whole number.
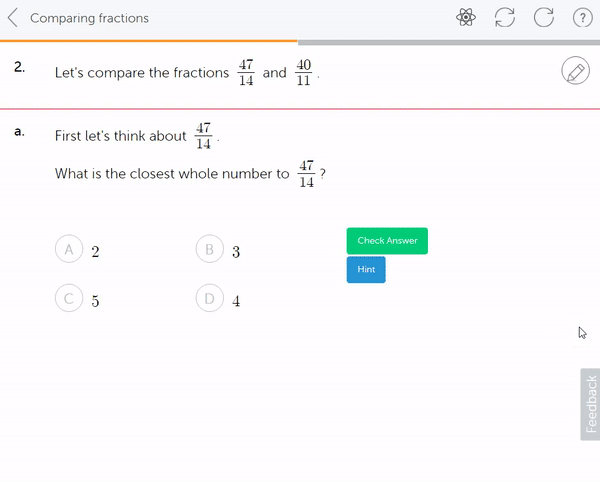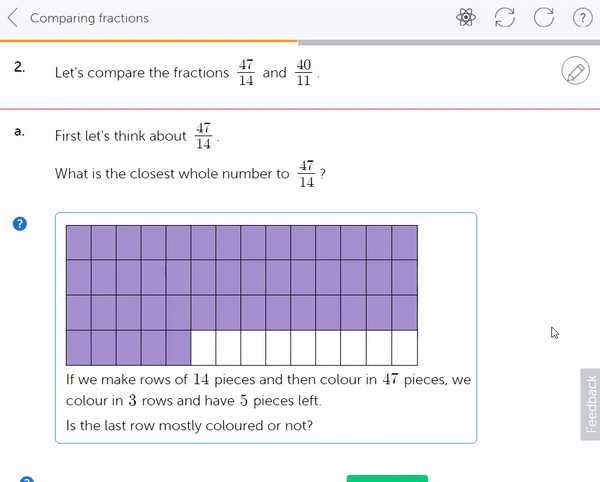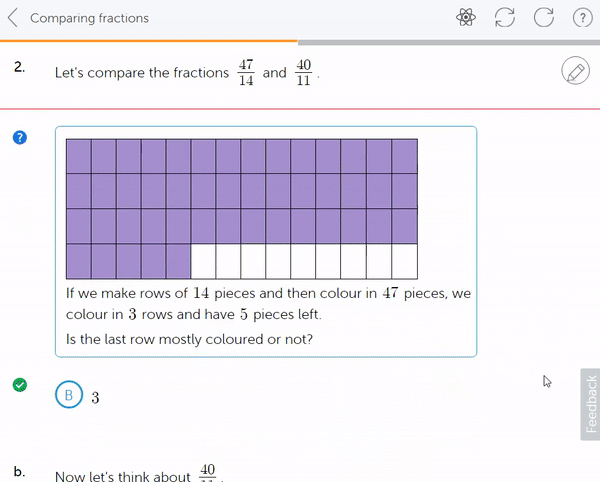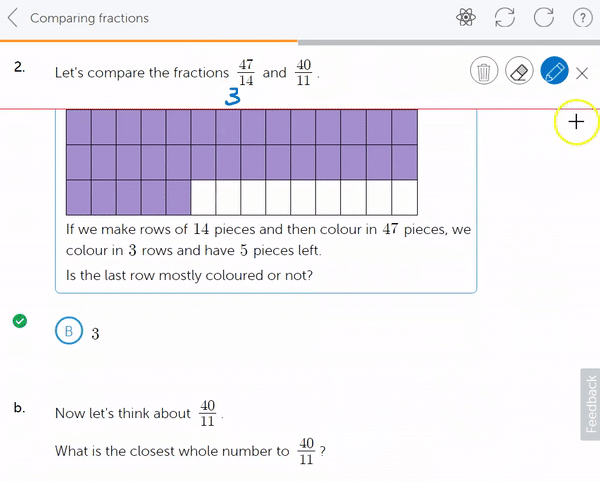
6a. Then, when the curriculum moves on to introduce addition of fractions, mixed numbers are integrated here. Starting with recognising that a mixed number is already an addition of sorts, that 1⅕ is 1 whole and 1 more fifth.
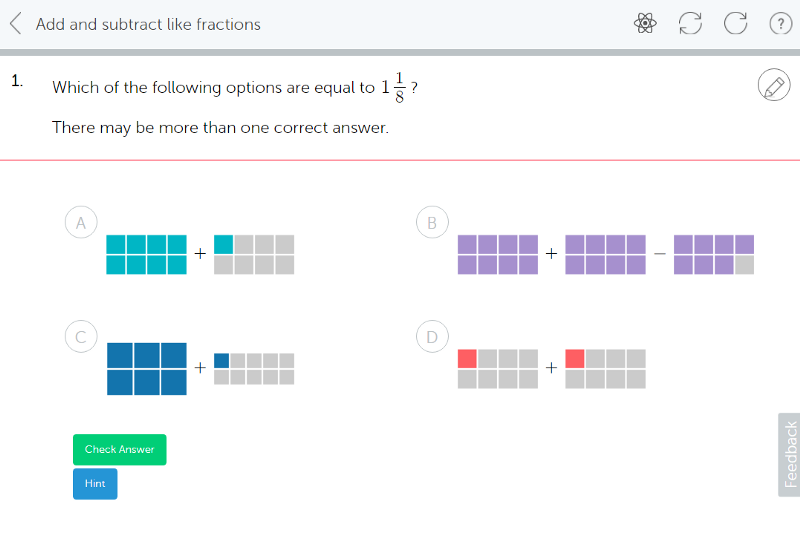
Addition is scaffolded well, starting from converting final answers between improper and mixed numbers.
2 thirds + 5 thirds is 7 thirds,
which is 7/3
which is 2 wholes and 1 more thirds.
The integration of the conversion from improper to mixed at this stage is essential for developing strong number sense around the size of the number 7/3. We can see from its mixed number version that it is larger than 2 wholes, but less than 3 wholes.
A more advanced number sense idea here, would be that it is bigger than 2 wholes but smaller than 2 ½.
6b. We now introduce the idea of adding and subtracting mixed numbers. We do this in a similar way to how we develop decimal addition and subtraction that usually comes a few years later, and that is through the understanding that 2 1/4 + 4 1/4 is pictured…
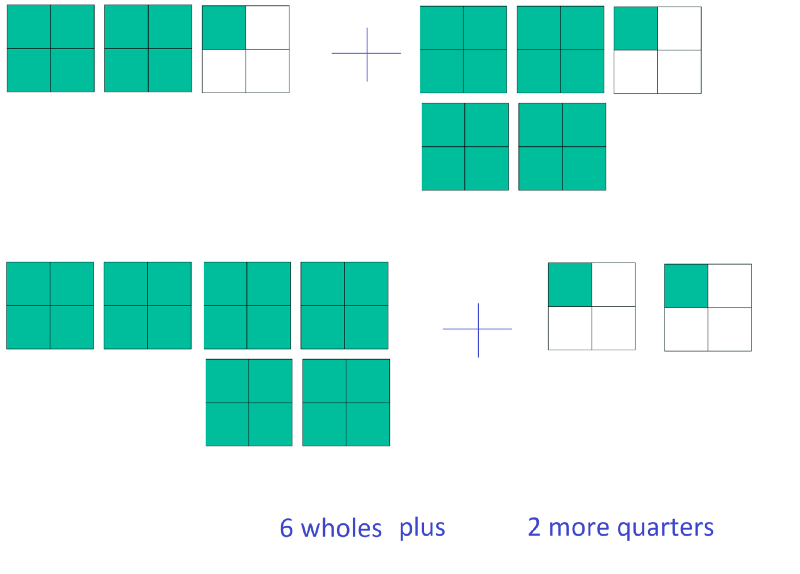
Some students can at this stage connect 2/4 to be the same as ½.
Generally the approach to elicit understanding here is to consider the whole-number parts first, followed by the fractional parts. This approach also yields a good estimation prior to the calculation. 2+ 4 is 6, so we must be more than 6. Both fractional components are less than ½ so the sum must be less than 7.
Resist here the procedural approach to convert both fractions to improper and then add them, it detracts from the intuitive nature of what is occurring. The convert first approach should be something that students recognise as efficient when adding or subtracting more complicated examples such as
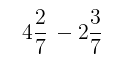
Although it could be argued here that a reasonable partition could be made,
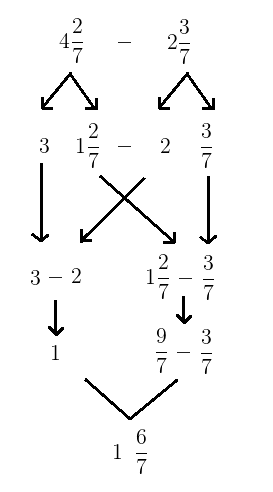
None of which is nicely formatted for a “pretty written answer”, but the reasoning is deep and connects all the ideas and strategies of whole number partitioning to fraction computation.
Why do we stop using mixed numbers?
Those that are familiar with higher level mathematics, would know that beyond this introduction in the early/middle years that mixed numbers are rarely if ever used in formal mathematics. Mostly improper fractions are used and kept for calculations. Why is this?
Well one reason is that in younger grades we spend far more time adding and subtracting, and mixed number representations can be quite useful here. i.e. Adding and subtracting whole number components first then adding and subtracting the fractional components.
They are also useful in developing the number sense associated with the different representations. For example, 1⅖ and 7/5. The 1⅖ immediately recognisable in size as something between 1 and 2. The 7/5 immediately recognisable as greater than 1 whole, and something that is made up of 7 equal size parts. It is also easier to see from the mixed number representation of 1⅖ that it is less than 1½. So an estimate for a computation using addition and subtraction using mixed numbers can in some ways be easier to arrive at.
In latter years we do more with multiplication and division, and we rarely keep mixed number representations in these types of calculations, in fact algorithmically, we convert mixed numbers to improper at this stage and then multiply, or invert then multiply as needed. So it isn’t necessarily that we stop using mixed numbers, more that our usage of them becomes less important in our formal mathematical studies.
Final thoughts
One thing that might be missing here is the bridge between what is perceived as primary usage, and secondary non-usage. Maybe we need to have students explore this deeply to understand how one representation is more useful in some situations than others? Then this gap in understanding about why we seem to use mixed numbers in earlier years and not use mixed numbers in older years might not exist.
So mixed numbers have their place, it’s great to develop that sense of size and we do need to be able to convert them for computation at different points in study. Some argue that mixed numbers are more real life, for example in recipes and in dividing physical quantities between people. So maybe mixed numbers have greater importance in a numeracy perspective, and improper have greater importance in formal mathematical calculations?
Either way, curricula from around world follow a very similar pattern in the development of mixed numbers and we all do it at about the same time in schools. What we can benefit from here is understanding how the importance of exploration, play and conversation can be in drawing out the conceptual understanding of what mixed numbers are, and in relating the relevance of mixed numbers to the context, the calculation or in estimation and assessing reasonablness.
Thanks to Andie Hoyt.

