Mathematically Perfect Gift Wrapping -Explained

If you don’t like wasting gift wrapping paper (and we sure don’t), then this is the perfect post for you!

Recently we asked if it’s possible to achieve mathematical perfection when wrapping gifts.

Let’s start by considering how most of us would wrap a gift that’s in the shape of a rectangular prism (such as a book)…

We cut a rectangular piece of wrapping paper, fold the wrapping paper to cover the largest face, and end up with a lot of overlap!

How can we wrap the same gift with less paper?

One logical approach is to use just enough paper, so that the two sides covering the largest face just meet (no overlap).

The issue with this approach is that you still have quite a bit of excess paper (outlined in red below).

Is there a way of wrapping with even less wastage?

The two approaches above have used a rectangular piece of paper. What if we use a square piece of paper and turn the gift about its centre, so that the edge of the face makes a 45° angle with the edge of the square of paper?

For a book with dimensions l x b x h, we end up with the book laid out on the wrapping paper as shown below.

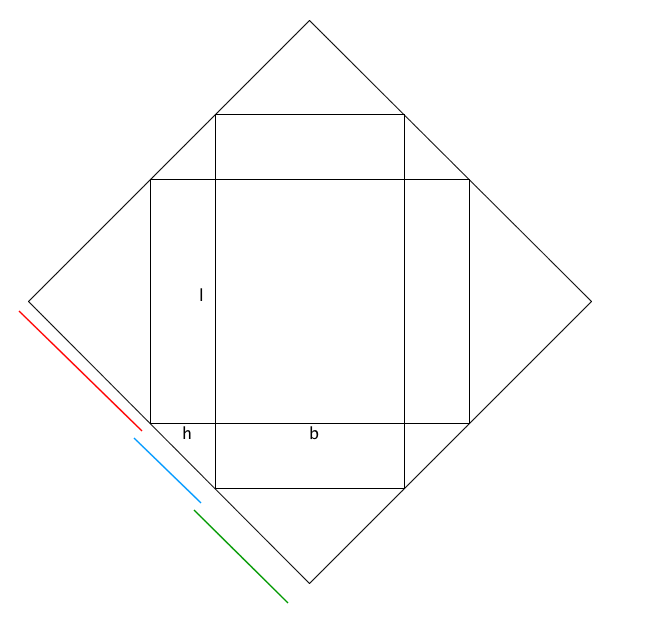
So what is the length of the sides of this square? The green segment has length equal to half the diagonal of a square of sides b, the red segment has length equal to half the diagonal of a square of sides l, and the blue segment has length equal to the full diagonal of a square of sides h. Overall, its dimension is 2( (l+b)2 + h ) to each side.

But does this square actually wrap the present? The answer is yes! The “wasted” paper is highlighted in the image below:

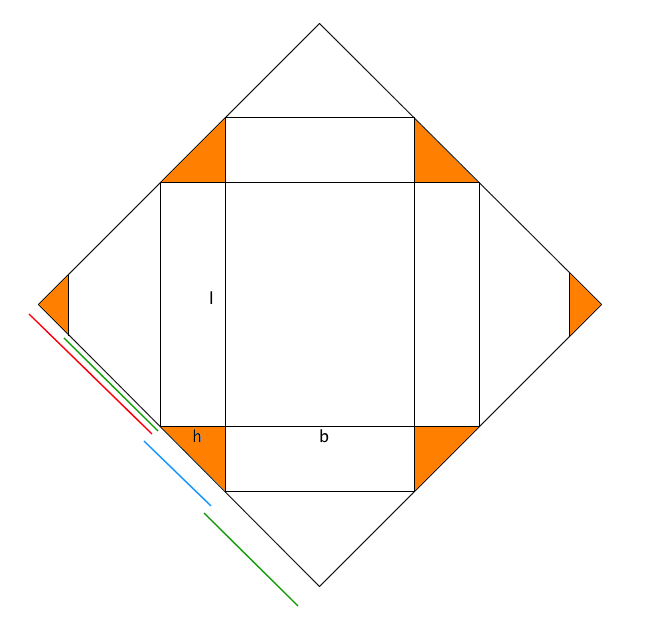
There is very little waste, and in the case where l=b the corners meet together perfectly in the middle.

So when you come to wrap your own gifts, put the largest face down on the paper, aligned so the edge of the face makes a 45° angle with the edge of the square of paper. Make sure each corner of the paper folds up to cover each side fully, and fold it all together over the top.

But there is one question remaining…

What happens if the dimension l is very very big, and the other two dimensions are small?

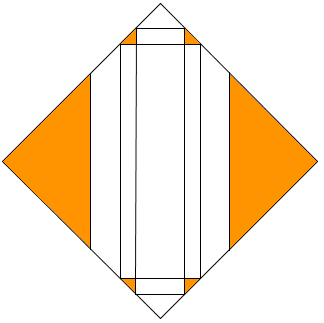
That’s a lot of waste… using a rectangle in the more “traditional” way ends up using less paper. When do you decide whether to wrap it like that, or with a square as described in this post?

Share your ideas below!