Just go with the flow: The math of fluid
The Coffee + Math Series

We have a team full of mathematicians, math teachers, and math enthusiasts. We want to share our passion for math with everyone, so we’ve decided to launch a new series called Coffee + Math.
Coffee + Math is as simple as it sounds. We have a coffee and chat about our favorite math equations, math facts and other math tidbits.
This week we grabbed a coffee with Jake Horder, resident mathematician and qualified environmental engineer, to find out more about his favorite math equation.
Coffee of choice?
Single origin, black, no sugar.
What’s your favorite math equation?
My personal favorite is the Navier-Stokes equation.
Draw it for us!

Ok… Can you translate that into English?
Sure! Imagine that your coffee is made up of lots of tiny parcels of fluid.
What are the ways each parcel can change over time?
Hint: A parcel can move, stretch, twist or spin depending on the forces applied to it.
The left hand side of the Navier-Stokes equation is the inertia; a measure of how difficult it is to change the speed and direction of the parcel.
The inertia is made up of terms describing how the velocity changes in time and space.
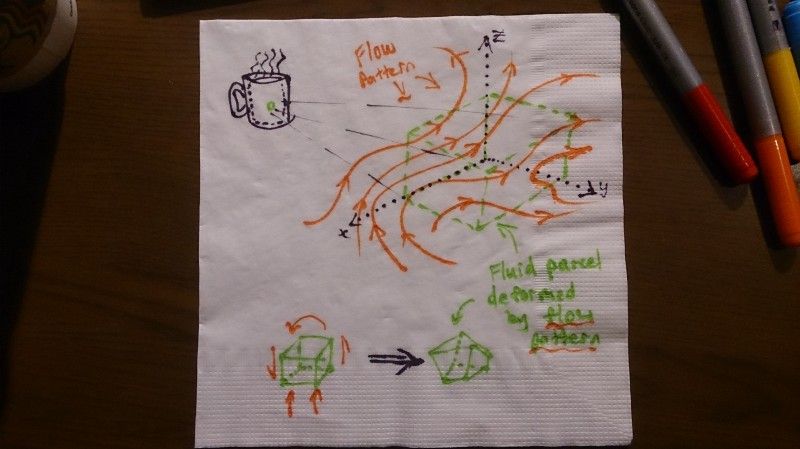
The right-hand side of the equation contains the forces that act on the parcel, the things that might make it move and twist and deform. These include the surface forces like pressure and friction from the neighboring parcels of fluid as well as the force on the whole parcel due to gravity.
If we add up the effect all the parcels have on each other as they move around inside the mug then we get a description of how the coffee as a whole behaves.
The Navier-Stokes equation is essentially Newton’s Second Law, F=ma, but for fluids.
Why are you so interested in this equation?
I started sailing when I was quite young. I picked up a lot of my skills from fellow sailors, yet I often felt like I was following rules without really understanding why.
Why did the boat have to point this certain way? Why do the tell-tales need to be straight? Why is there a secondary sail in front of the mainsail (the biggest sail)?
Years later I realized that a lot of my sailing skills could be explained by the study of physics and mathematics.
It was genuinely exciting to find connections between what I was learning during my university fluid mechanics classes, and what I had always wondered about in my everyday life.
A plane wing acts to turn the direction of a flow field, constantly throwing air downwards, which in turn lifts the plane upward (see Newton’s third law of motion). Of course this is the same as the mainsail on my Hobie catamaran, which curves the wind around it to pull me along the water.

I think about a flag fluttering in the breeze, the periodic back and forth as turbulent vortices tumble along each side. Clearly the very same phenomenon rustles up my mainsail if I point too high into the wind, the air can’t stick to the sail anymore and begins to trip over itself.
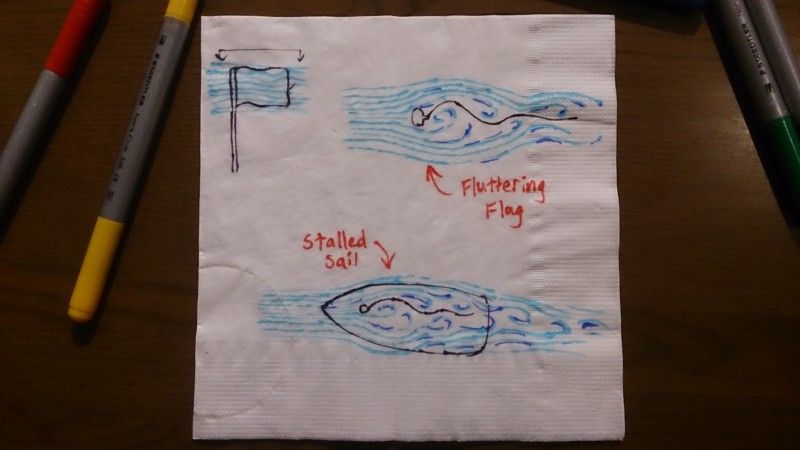
These and many other everyday encounters with fluids all descend from the ideas captured by the Navier-Stokes equation. I feel that a deeper understanding of the nature of fluids emerges from being able to read the mathematics in the flow. And so far it has been a very satisfying journey.
How is this equation useful outside of sailing?!
Fluids are everywhere. Knowing about the equation of fluid motion can give us a greater understanding of a lot of cool natural phenomena.
Is oobleck a solid or a liquid? What does a year of global weather look like? How does a spiral galaxy form?
We can also use the Navier-Stokes equation to guide us in designing efficient structures, machines and devices that are immersed in or contain fluids. We can consider the flow of air past a wind turbine, build a faster bullet train, or even model how blood might move through an artificial heart.
Without knowledge of the Navier-Stokes equation, the only other way we could design these things is by guess-and-check, and that gets very expensive (not to mention time-consuming)!
Can you tell us about the history of this equation?
Our very existence is dependent on water. So the study of how water, and other fluids behave, dates back thousands of years.
Archimedes and other ancient Greek thinkers made many important observations using the mathematics and technology of their era, but with Newton’s invention of calculus in the 1600s, a more sophisticated mathematical toolbox was available to scientists like Claude-Louis Navier and Sir George Stokes to fine tune our understanding.
Navier was a French engineer who pioneered the study of how structures bend, twist and deform and he went on to apply the same ideas of stress and deformation to fluids. In the 1840s it was Stokes who, among many other achievements, formalized this relation mathematically into the familiar Navier-Stokes equation.
Anything else to add?
Well, yes actually.
There have been many attempts to find useable solutions to the equation, methods to tease out the variables of interest like the velocity and pressure fields. This is extremely difficult and currently there is still no known solution to the full Navier-Stokes equation — we don’t even know if one exists!
This means that today most of the applications use numerical approximations of the equation that are then solved by very powerful computers. This is an interesting area of study in itself and is known as computational fluid dynamics.
But here’s something interesting… If you can find a solution to the full Navier-Stokes equation then the Clay Mathematics Institute will give you $1,000,000.
So stop reading, and start trying to find a solution to this equation!

