How to make an infinite amount of money (and other things Statistics can prove)

The Coffee + Math Series

This is our second instalment of the Coffee + Math series. It’s simple - we have a coffee and chat about our favorite math equations, math facts and math tidbits. What more could you want?
This week we had (an almond milk) coffee with Jack Freestone, resident Mathspace mathematician and uni student (majoring in advanced mathematics).
Coffee of choice?
Double-shot almond milk latté.
Really? Almond milk?
Give me a break.
What’s your favorite area of math?
Definitely Statistics and Probability Theory.
Can you give us an example?
I’ve actually got a pretty good example! I can use some Probability Theory to show that it’s possible to make an infinite amount of money in a game of chance.
Umm, hello! What are you waiting for?
There’s a concept known as the Gambler’s Ruin Problem which can show it.
Imagine that you have $n and you decide to play a game where each round has a chance that you’ll earn $1 with probability (p) or that you’ll lose $1 with probability (q).
Now after one or two rounds the earnings seem pretty slim, but what’s cool is that you could become infinitely rich. It’s possible, so long as you play an indefinite amount of rounds, and the chances of you winning are at least slightly in your favor.
Can you give us a step-by-step breakdown?
Sure. Let’s say that, with your $n, you keep playing until you either reach $N or you end up broke with $0.

In this case, the probability of you reaching $N starting from $n can be expressed as the following:
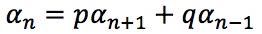
The left hand side is the probability of reaching $N starting from $n. The right hand side translates to “the probability that you’ll win the first round and then reach $N now starting with $n+1 OR that you’ll lose the first round and reach $n now starting with $n - 1.”
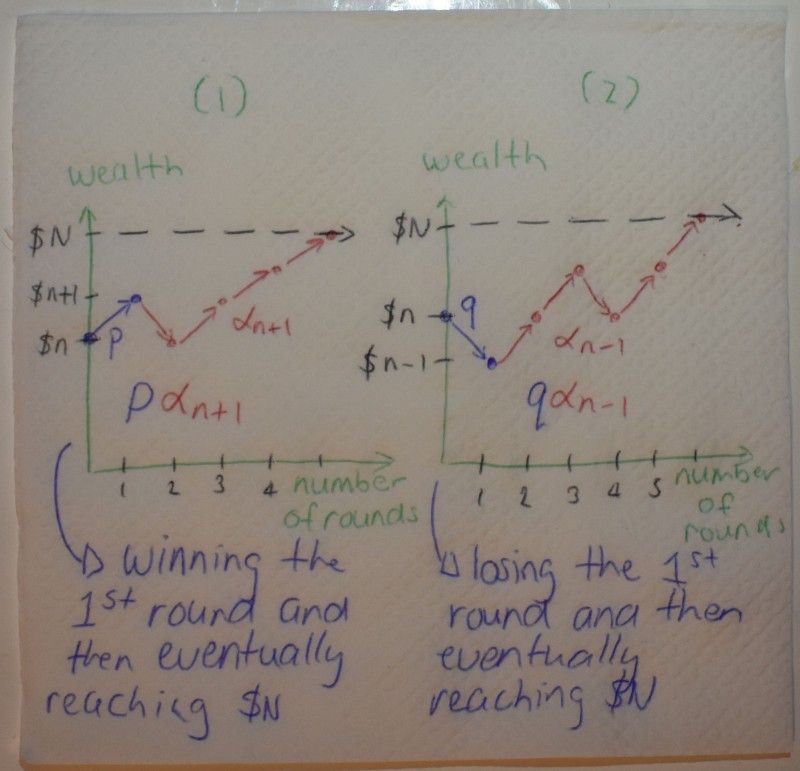
Now, since p + q = 1, the above equation becomes:
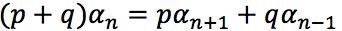
After some rearrangement:
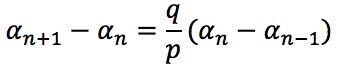
And with some recursive substitution:
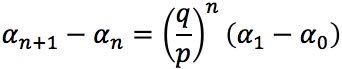
Since the likelihood of reaching $N starting from $0 is zero:
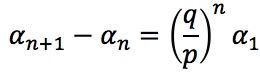
As an aside, we can make two statements about the probability of reaching $N, now starting from $N:
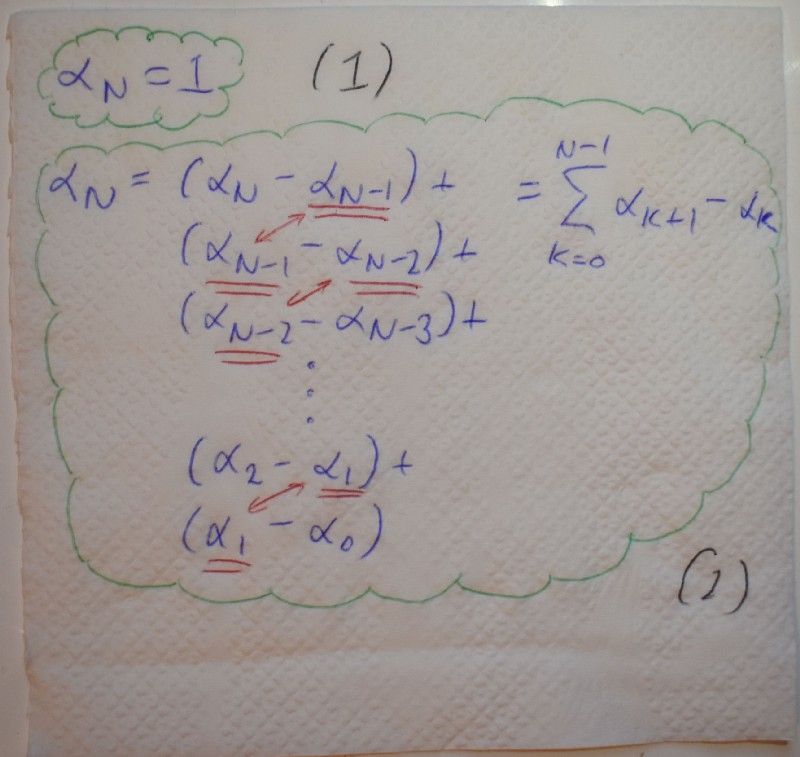
The first statement says that the probability of reaching $N starting from $N is 1.
The second statement uses the cancellation of consecutive terms (except for the first and last) to rewrite the probability of reaching $N starting from $N.
Substituting equation (1) in the second statement we get:
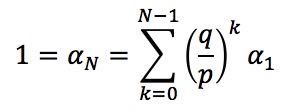
And with some rearrangement:
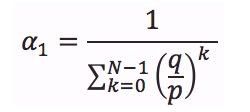
Using the same procedures above, we can reach the following equation:
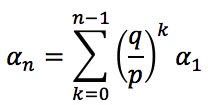
And by substituting equation (2), we get:
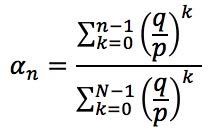
Now let’s assume each round is slightly in your favor, i.e. p > q.
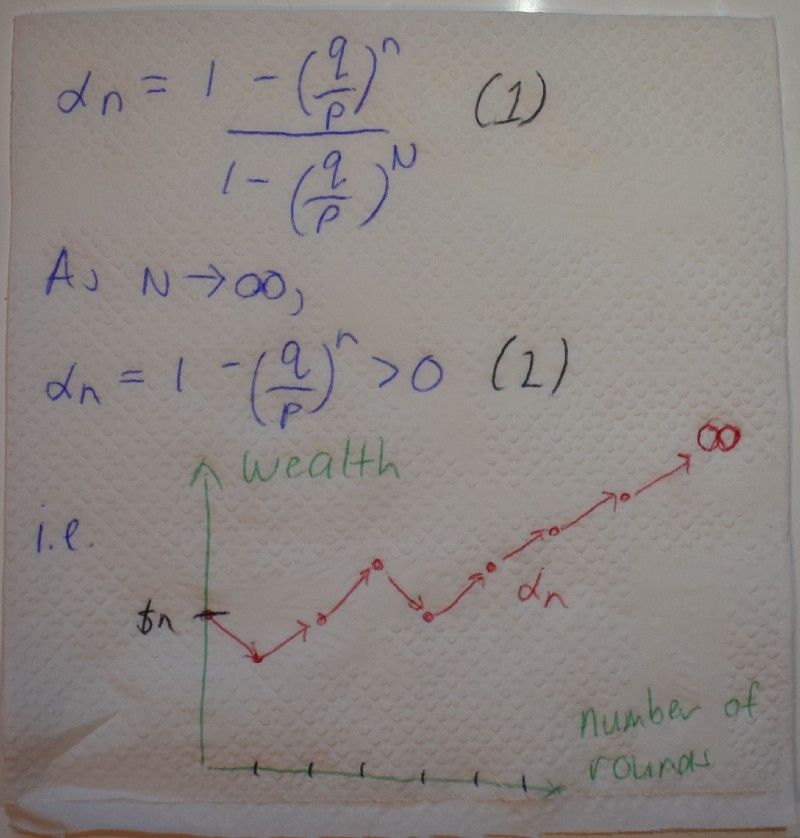
The first statement in the above diagram uses the fact that the numerator and denominator is just a geometric sum.
The second statement lets $N approach an infinite amount of wealth, in which case, the denominator becomes 1.
The final result shows a positive probability for the likelihood of you successively earning an infinite wealth starting at $n.
To shed light on this result, consider the weight imbalance of a coin. It’s proposed that there is a 51% chance of the coin landing on the side that’s facing up before it’s flipped. Say you enter a game starting with $100 where each round is a coin-toss. As before, if you guess the outcome of the toss correctly, you earn $1, and if not, you lose $1. If each round you choose the side facing up before it’s tossed, your chances of earning an infinite amount of money (if you can live as long) is more than 98%.
So basically, it’s possible, but you’d have to live forever?
Pretty much!
Why else are you interested in Statistics and Probability (aside from figuring out how to make infinite amounts of money)?
In between the many classroom jokes and tangents at school, it was my teachers that stirred my initial love for both Math and English. My interests in both subjects continued into university, with the majority of my units being Statistics classes, with the odd arts unit thrown in. Many people think that the two disciplines (Math and English) are at odds with one another, but I disagree.
Logical processes involving language and numerical statements are more closely linked than you might think. In many ways, Statistics is where the ‘imaginative world of English’ and the ‘factual world of Math’ meet.
Statistics works in a very mathematical way (with its notation and rigorous derivation), but a great deal of creativity and imagination lies beneath it.
The Gambler’s Ruin Problem incorporates some creative algebra and a probabilistic understanding of the world. The lengthy mathematical equations used above are simply a way of presenting these ideas.
The interesting thing about the results in statistics is that they can often go against our ‘gut instinct’. They can shock us, and encourage us to delve deeper into what they mean. It’s like a surprise plot twist in a well-written novel!
I still find myself surprised by the result in the Gambler’s Ruin Problem, but in light of its derivation and further thought, I am comforted by its correctness and feel as though I’ve gained some deeper understanding of how the world works.
Why is the area of Probability and Statistics so important?
We’re living in data-driven times, and people are really starting to appreciate the importance of Probability and Statistics.
Probability and Statistics have led to many discoveries and innovations, enabling policy makers, business people and educators to make data-based decisions. It also plays an important role in disciplinary fields that aren’t immediately considered Math-oriented, such as Psychology, Biology, Anthropology and Epidemiology.
Often in our daily lives we come face-to-face with statistics without even realizing it. For instance, say you flipped a fair coin one hundred times, and each time, it landed on heads. The immediate response for some is that surely it won’t land on heads in the next throw. And yet, it does. This is because the coin has no memory that it previously landed on heads one hundred times, and your chances still remain the same, about 50/50.
Can you tell us about the history of Statistics & Probability Theory?
Whilst statistics wasn’t formally developed until the 17th century, many unknowingly used it long before that.
Al-Kindi was a philosopher and mathematician who wrote a book called Manuscript of Deciphering Cryptographic Messages in the 9th century. He explained that an encrypted message written in a particular language could be deciphered by referring to the frequency distribution of letters that appear in that language.
There are a few tools for creating your own encrypted messages, using the same idea as above.
The history of Probability Theory stems from games involving chance. A notable example is called the Problem of Points. The solutions to the problem can be accredited to Blaise Pascal and Pierre de Fermat during the 17th century.
The problem asks, how could the stakes of a game be fairly divided between two players if the game was interrupted at a certain round? Several mathematicians have proposed solutions, however, the fairest way of dividing up the wealth for player 1 and player 2 is in the ratio of:
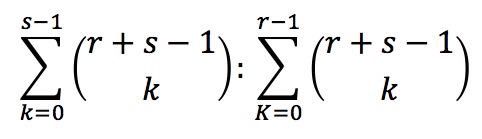
Where r and s are the number of successful rounds player 1 and player 2 need in order to win.
The left hand side of the ratio captures all the ways player 2 might only win 0 rounds + 1 round + 2 rounds and so on up to s - 1 rounds. In any of these cases, player 1 will win. The right hand side, by symmetry, has a similar result for player 2.
The use of discrete combinatorics and the concept of chance motivated the field of Probability Theory.
Anything else interesting to add?
What I love about Statistics and Probability is that it is such an accessible field of study. This is because it largely relies on intuition and conceptual thinking, as opposed to lengthy equations and prerequisite knowledge.
I’ve pulled out some of my ‘top reads’ below for anyone interested in knowing more about the field.
Say that you’ve been positively diagnosed with a disease. What is the chances of you actually having it? Bayes has an answer and the results may not be a cause for concern as you might think!
How can we assess your approach to risk? Let’s make a bet. I’ll give you $12 if this coin lands on heads. If it lands on tails, you give me $10. Don’t want to take the bet? How about if we play 100 times? Will this change your answer?
David Aldous’ script for his talk at Cornell University, 2004.
David Aldous opens up some interesting points on Probability Theory discussing the psyche of individuals and the misconceptions of coincidence.

