How far away is the horizon?

Imagine you’re at the beach, standing on the shoreline (lucky you!).

Off  in the distance you see a ship on its way out to sea. Slowly it appears  to get smaller and smaller, until it drops over the horizon and out of  sight.

How  far away does the ship get before it starts to disappear? In other  words, how far away is the horizon? Take a guess… 6km, 10km? More? Maybe  less?

The good news is, we can work it out!

Picture  a line, starting from your eyes and going straight all the way to the  horizon. We’ll call the length of this line d. Once we know what d is in  terms of numbers, we will know the answer to our question!

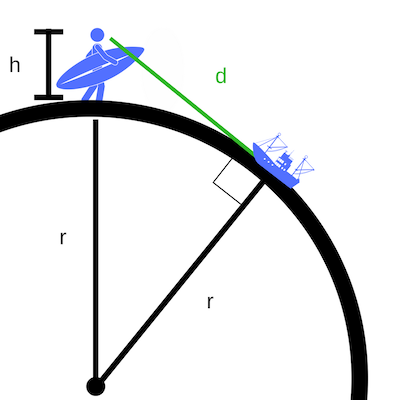
So which measurements do we need to find ‘d’?

Imagine  a second line, also starting from your eyes, but going straight down,  through the ground, all the way to the centre of the earth.

The length of this line will be your height, h, plus the radius of the earth, r.

We’re  going to need one more line — this one starts at the end of the first  line (at the horizon) and goes to the centre of the earth, so its length  is also r. This gives us a right-angled triangle, as shown above in  Figure 1.

Checklist

1. Your height (we’re using 1.5 m in our worked example below)

2. The radius of the earth — You can find this by searching the web. It’s 6,371 km (or 6,371,000 m)

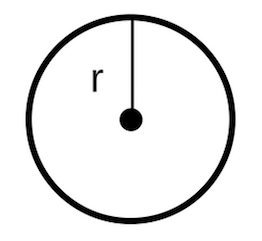
Now for the calculation

We know that the lengths of the sides of a right angle triangle are related by Pythagoras’ Theorem. So we have:

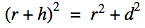
And by rearranging to solve for d, we get:

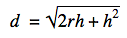
Everyone  knows their height, and the internet knows the radius of the earth, so  everything on the right-hand side is ready to go. Let’s try it out.

Suppose  you’re 1.5 m tall, and standing at sea level — this means you’re about  6,371 km, or 6,371,000 m, from the center of the earth.

Then…

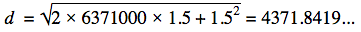
So the horizon is 4,371.8 m or 4.4 km away!

Try putting your own height in the formula to find out how far away the horizon is for you.

What else can you solve?

1. The  distance to the horizon changes as we change our height above the  surface of the earth. How far away would the horizon be if we were  standing atop the Sydney Harbour Bridge (h = 134 m), or at the summit of  Mt Everest (h = 8,848 m)? What if we were orbiting in the International  Space Station (h = 40,000 m)?
2. We  can also see that the distance depends on the radius of the Earth. In  fact, this formula would be suitable for any spherical object. How far  away is the horizon if you’re standing on the Moon (r = 1,737 km), or on  Mars (r = 3,390 km), Jupiter (r = 69,911 km), or the Sun (r = 695,700  km)?

So there we have it… Who’d have thought geometry could come in handy at the beach?

We’d love to hear of other ways to apply Pythagoras’ Theorem! Share below.