Happy Pi Day 2021

Every 14th of March (3/14) mathematicians and math lovers around the globe recognize and celebrate International Pi Day.

π is a mathematical constant, mostly known for its definition as the ratio of a circle's circumference to its diameter. But, it appears in numerous formulas across mathematics and physics.

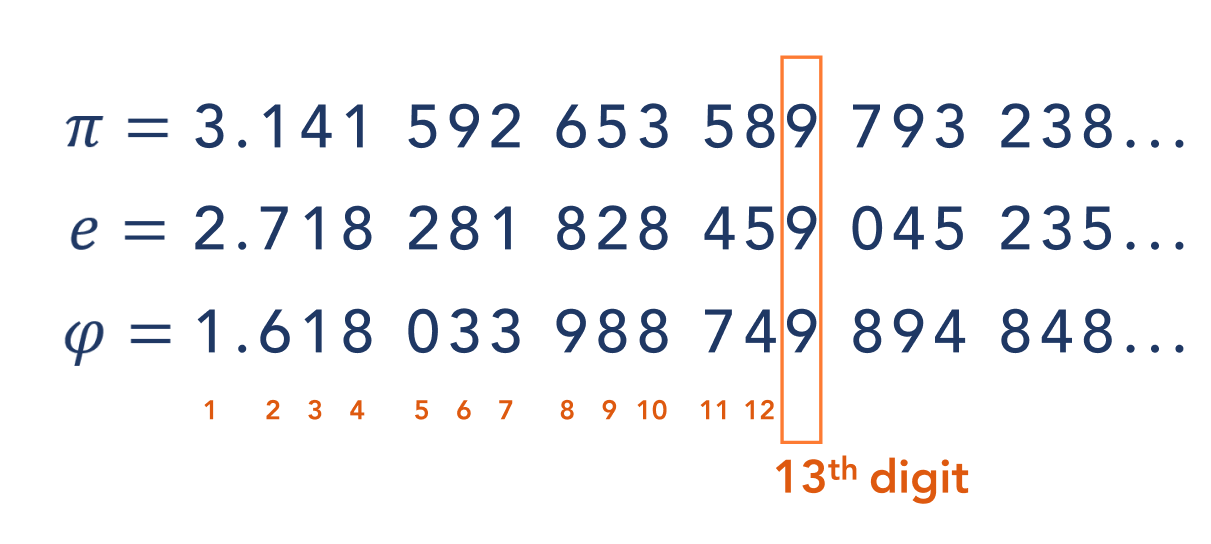
Pi Day 2021 is unique in its own way. The two-thousandth and twenty-first (2021st) digit of each of the constants π (pi), e (Euler's number), and φ (the golden ratio) are all equal to the same digit – in this case 3.

For the example above we have used the notation n to denote the nth digit of each constant. For example, π=3.141592…… thus,  π1=3, π2=1, π3=4, etc. And similarly, en and φn denote the nth digit of the mathematical constant e, also known as Euler's number, and φ the golden ratio respectively.

The first time this occurs is at the 13th digit:

What are the chances of the digits in the constants π, e, and coinciding?

To calculate the chance of the digits of the three constants coinciding, imagine if I choose a number between 0 and 9, what is the chance of you randomly selecting the same number? What is the chance of a third person also selecting the same number? Given the events are independent, we can multiply the probabilities.

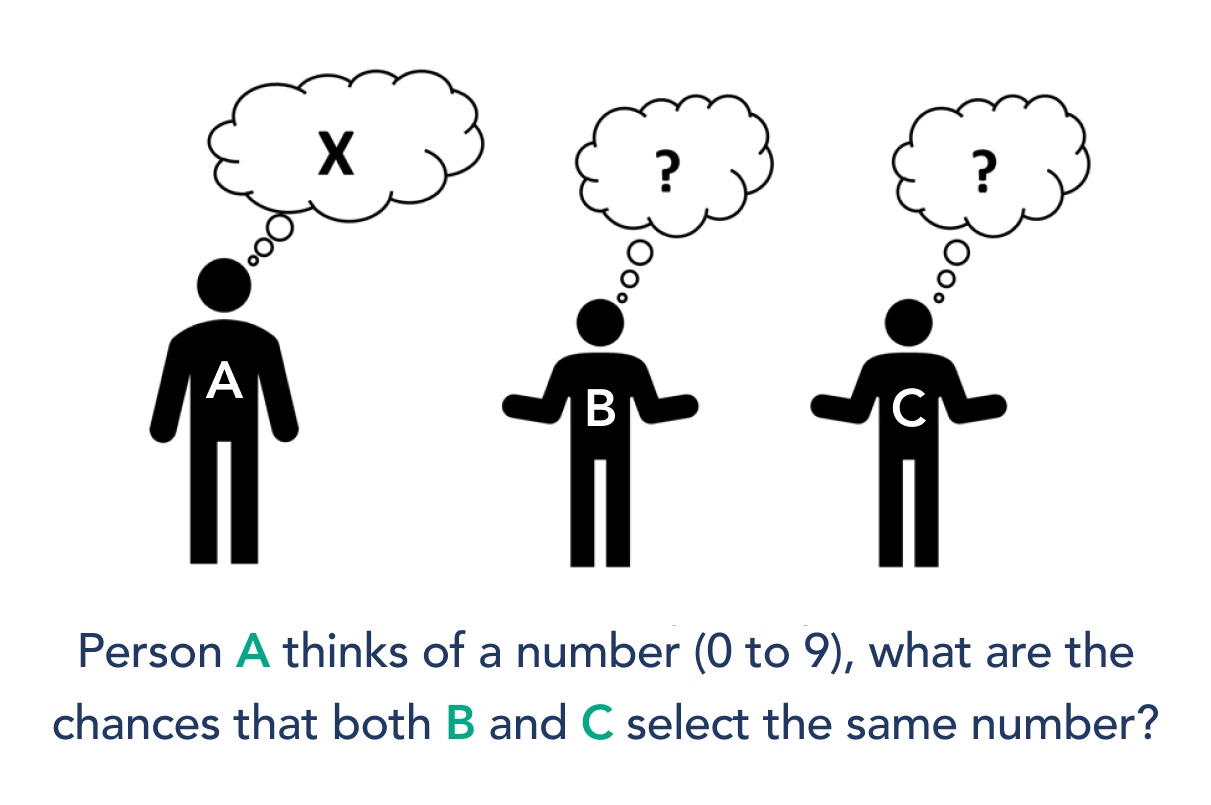
The digits of π,e, and Φ are independent and each digit is equally likely to appear at a randomly selected location. So finding the chance of the digits of the three constants coinciding is analogous to the above situation.

This calculation assumes that the digits 0 to 9 are uniformly distributed in each of the constants. That is, we assume each digit has an equal chance of appearing at a randomly chosen location. This in itself is an interesting investigation. To explore this, you could obtain a list of the first 100 digits of each constant and look at the relative frequency of each digit 0 to 9 occurring. Are they equal or do certain numbers appear more often? This can be extended with technology to look at the first 1000 digits or more and see if this assumption is reasonable. Given the probability of the digits of the three coinciding, how many times would you expect this to occur before the 2021st position?

Pretty cool, right? Read on for some more math fun with the number 2021!

Consecutive

Concatenation is the joining of two things together (for example, you can join numbers or letters) for a particular outcome. 2021 is not just a the  concatenation, but the concatenation of the consecutive integers 20 and 21. This hasn’t been seen since 1920 and won’t be seen again until 2122. This year also has the property of being the product of two consecutive primes (43 x 47).

When will be the next year that is the product of consecutive primes? What is the smallest integer that has both properties?

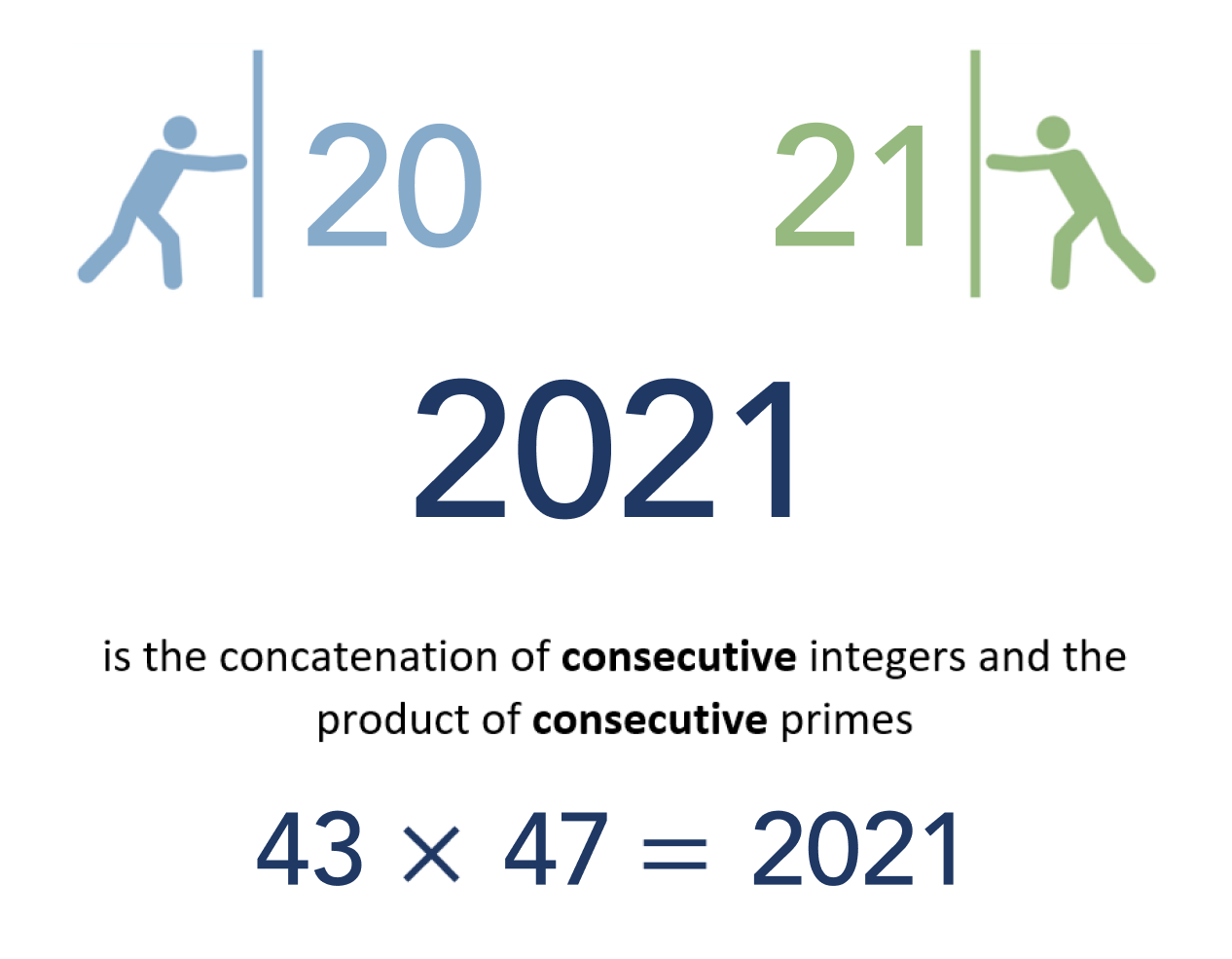
Palindromes

Palindromes aren’t just for students named Bob and Hannah or places like Glenelg and Aramara. We can also have palindrome numbers which read the same forwards and backwards. While 2021 itself is not a palindrome, when you multiply 2021 by its reverse you indeed form a palindrome. This is also true of the year 2011 but will we see this property again this century?  

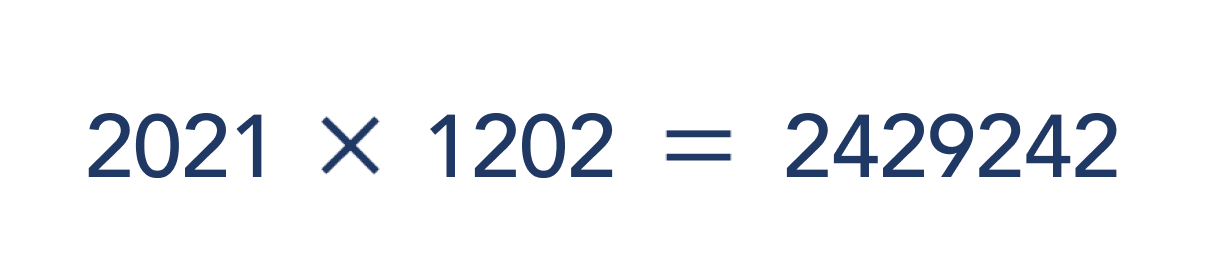
As well as palindrome years there are also palindrome days. Palindrome days fall on any dates where the numbers of the day, month, and year (or month, day, and year) are the same both forward and backwards, depending on the date format you commonly use. For example, the 30th of November 2003, (30/11/03) was a Palindrome Day for the date format DD/MM/YY.

How many palindrome days will occur in 2021? Do we have any that include the full year like we had on the  2nd of February 2020, (02/02/2020)? This date in 2020 had a rather unique property of being a palindrome date in both the MM/DD/YYYY and the DD/MM/YYYY date formats. Will you see another such date in your lifetime?

Loop

1. Start with 2021
2. Reverse it
3. Square the new number
4. Reverse that number again
5. Square root the number
6. You should end up with 2021

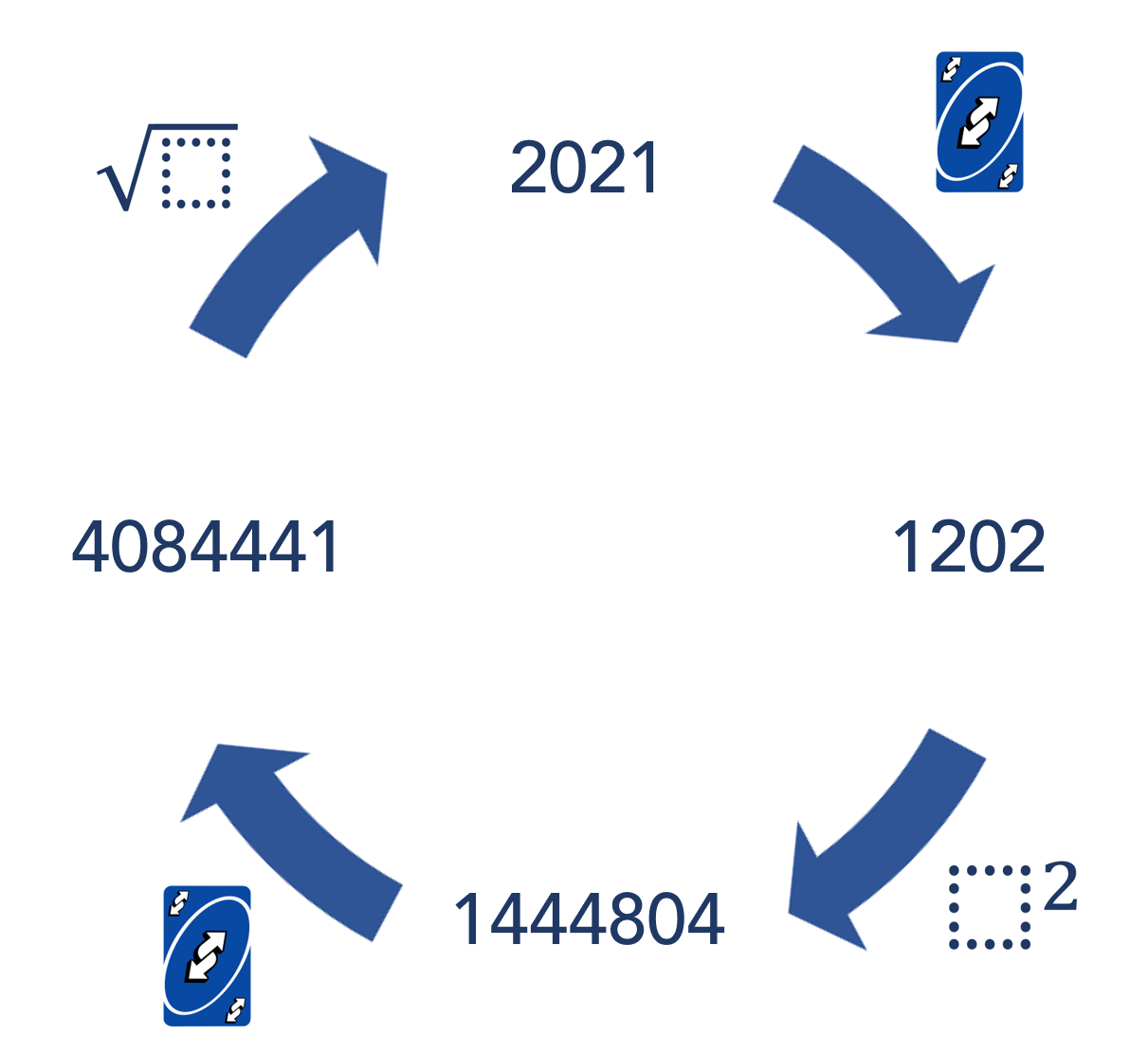
At a glance this might appear a little trivial as we have two reverses plus a square and square root, operations that undo each other, however, since these operations do not follow each other this property is in fact unusual.