Going down the rabbit hole

Fibonacci’s Numbers are amazing, creative, fascinating and worth every second of this blog post.

This week we didn’t have coffee with our school liaison, Jonathan Templin, because:
a.) He doesn’t drink coffee and;
b.) He recently launched Mathspace Canada (so he’s based in Canada, and that’s a long way to go when you’re not even going to have coffee!)
Jonathan and his wife, Elisha, set up Mathspace in Canada at the start of this year. Both former math teachers, they’re now affectionately known as ‘Team Templin’ by everyone here at Mathspace. We hope you enjoy this great exploration of Fibonacci’s numbers as much as we did.
Coffee of choice?
My favorite coffee would have to be… no coffee!
I have never liked coffee, despite five years of university and another five years immersed in the coffee culture of Melbourne, Australia.
Favorite mathematical field of study?
There is so much to choose from, but I think the Fibonacci numbers would have to be near the top of my list. They are a sequence of numbers popularized by the Italian mathematician Leonardo of Pisa, aka Fibonacci, around 800 years ago.
Can you show us the Fibonacci numbers?
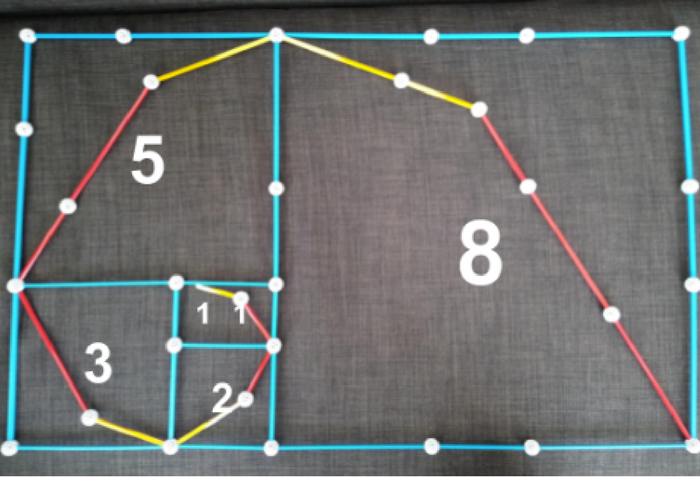
The Fibonacci numbers are 1, 1, 2, 3, 5, 8, 13, 21, 34… Sometimes, you’ll see a 0 as the first number in the sequence, before the two 1s. Can you spot the pattern?

Big sigh for the Dad joke above.
Sorry! That’s the teacher in me trying to encourage my students to discover math on their own.
Can you explain the pattern?
The pattern here is that, once you start with the first two numbers in the sequence, the next number is found by adding the two previous ones. That is, 1+1=2,1+2=3, 2+3=5 and so on. If you know two consecutive Fibonacci numbers, you can always figure out the next one.
Why are you so interested in this?
Ever since I was young, I loved patterns. I liked things that had a set structure and rule, and if there was chaos, I wanted to bring order to it. I loved following the instructions in a pack of Lego to create the latest underwater castle or Lego Mindstorms robot. This has followed me to my adult life, where I actually enjoy putting together Ikea furniture. The feeling of satisfaction I get from following finding order (a new coffee table) from chaos (boxes full of particle board, screws and nails) cannot be understated.
I find following a pattern to be very meditative, and discovering a new pattern to be a joyous experience.
If there is a seemingly random collection of data, I will look for the underlying pattern. For those of you that read my colleague Mansour’s musings on entropy, I will say that I would be the person to sit down with his second diagram of dots and try to find the formula.
The Fibonacci numbers at first look like a random jumble of numbers, but they follow a clear and simple pattern that can understood by anyone who understands how to add two numbers together. However, in all their elegant simplicity, the Fibonacci numbers can be used to provide structure to a wide variety of things, in mathematics and in nature. Once again, order from chaos.
Can you tell us about the history of the Fibonacci numbers?
While the Fibonacci numbers have been named after an Italian mathematician, it is worth noting that it seems likely that Leonardo would have seen the numbers in his travels in Africa or India, as there is evidence that mathematicians there had known of the sequence hundreds of years before.
In European circles, the Fibonacci numbers were introduced through Fibonacci’s book Liber Abaci. Interestingly enough, the example used to demonstrate the sequence involved breeding rabbits.
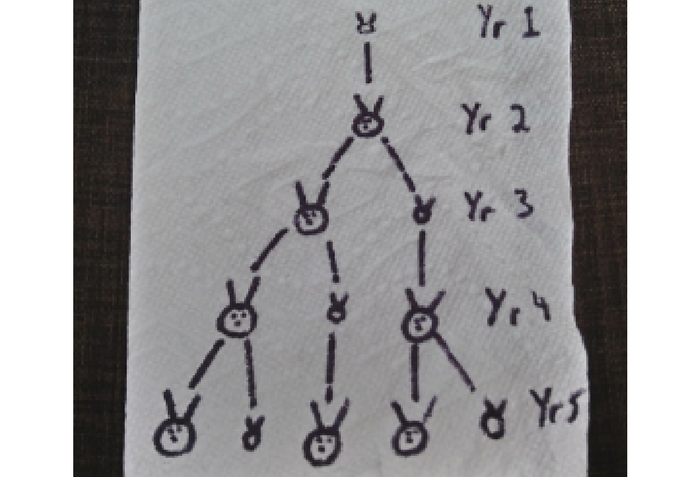
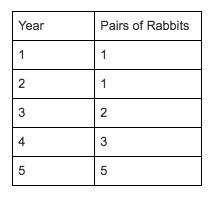
Initially, there was one pair of rabbits. In the simplified scenario that Fibonacci explained, a pair of rabbits cannot reproduce at first, but each subsequent year will give birth to a new pair of rabbits. In year one, there is one pair of juvenile rabbits. In year 2, that pair of rabbits is now mature, but there is still only one pair. In year 3, the original rabbits are still mature, and they have now birthed a new pair of juvenile rabbits, so there are two pairs of rabbits now. In year 4, our original pair gives birth again, but their first offspring has not bred, so there are now 3 pairs of rabbits.
One beautiful relationship that has been found is the relationship between the Fibonacci numbers and phi , the golden ratio, one of the world’s most mystical numbers.
For those who are not familiar with it, phi is approximately equal to 1.618. If you divide any pair of consecutive Fibonacci numbers by one another, the result of that division, or the ratio, will approach phi as you choose larger and larger Fibonacci numbers. For example, 3 and 5 are consecutive Fibonacci numbers, and their ratio is 5/3=1.6666… Additionally, 4181 and 6765 are also consecutive Fibonacci numbers, and their ratio is 6765/4181=1.61803…, which is an accurate representation of phi to 7 decimal places.
Earlier on, I mentioned that the Fibonacci numbers are found by adding the two previous numbers in the sequence, but what if you want to calculate the 100th Fibonacci number, or the 1000th? It would be a pain to have to manually calculate the first 99 or 999 numbers to get the next one. Thankfully, there is a formula to calculate the n^th Fibonacci number. The interesting thing is that this formula is closely is also closely related to the number phi.
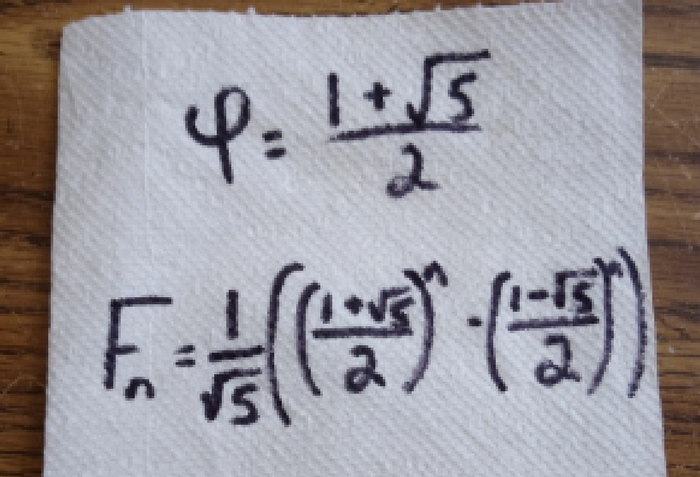
How do you think it will be useful in the future?
I have absolutely no idea! And to me that is one of the most beautiful things about mathematics. Sometimes, we do not study something because we expect it to be useful, but rather just because we want to. As a teacher, I loved answering the question:
When am I ever going to use this?
But sometimes I want to shout:
Probably never, but that doesn’t mean it isn’t amazing and creative and fascinating in its own right!
Sometimes I do math for the sake of doing math, and I’m proud of that. Some of the applications of the Fibonacci numbers were discovered hundreds of years after the numbers became popular. There is no way that Fibonacci or the early Indian mathematicians who popularized the numbers could ever have seen what they would become, but that didn’t stop them from investigating an interesting pattern, and it shouldn’t stop us from exploring the wonders of mathematics either.
Anything else interesting to add?
You can make your own “Fibonacci-like” sequence by choosing any two starting numbers, and following the Fibonacci rules to generate the rest of the sequence. For example, the sequence starting with the numbers 2 and 1 becomes 2,1,3,4,7,11… and has its own special name, the Lucas Numbers. Create your own Fibonacci-like sequence and see what properties it has. You never know what you might find!