Euler’s Identity: The Intersection of Math & Poetry

The Coffee + Math Series

Welcome to our Coffee + Math series. This  week we had an iced coffee with Andie Hoyt in St. Louis, Missouri.  Before finding her home at Mathspace, Andie was a high school Math  teacher. Now she helps to run our US School Success team AND she writes a  lot of the math questions that you find in Mathspace.

Coffee of choice?

Iced coffee in the summer and lattés in the winter.

Favorite math equation/fact/field of study?

So  many to choose from! I’d have to say Euler’s Identity is on my top five  list. I’m sure I’m not unique in having this as a favorite because it’s  simply beautiful once you understand it.

Beautiful?

Yes, I did say beautiful!!

What is Euler’s Identity?

It’s a formula. But that description doesn’t seem to do it justice. It’s SO much more than a formula!

Can you draw it for us?

You bet!

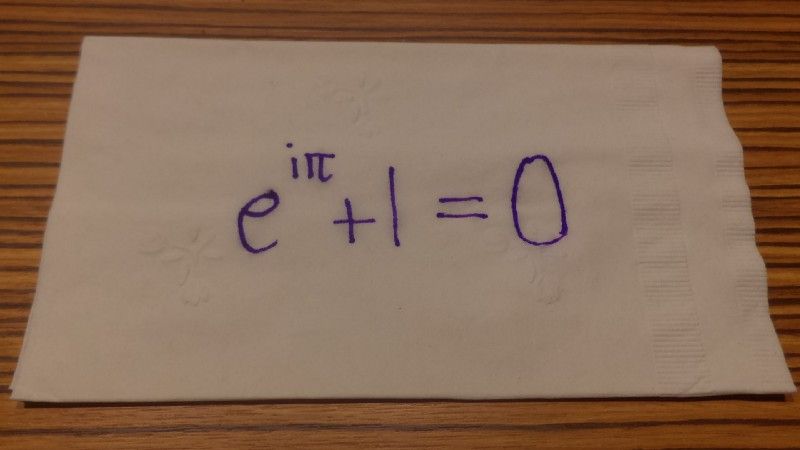
Can you explain that in English?

To understand the meaning of this relationship, you really need to understand the importance of each major character here…

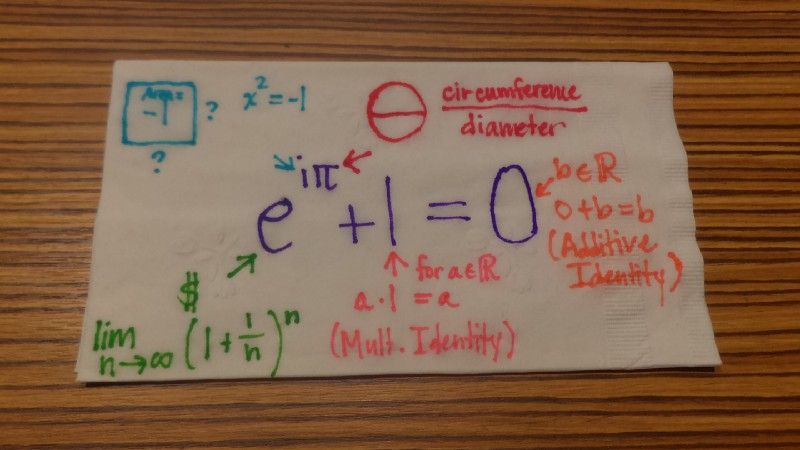
I’ll start with 0 and 1. Really under appreciated numbers in my opinion. But if you really think about them, they’re the principal roles. Add zero to a number, doesn’t change the number. Multiply a number by 1, doesn’t change the number. That’s pretty special!

We see the plot round out with the addition of Pi — an irrational number, that, ironically by definition is a ratio. Measure any circle’s circumference and divide that number by its  diameter and you always get the same number — Pi. But the fact that it’s  digits are unending makes it even more of a phenomenon.

It’s irrational to think that Pi would be the only character with unending digits in this story. The number e, is actually named after Euler himself.  If you’re interested in learning more about it you should study, well,  interest. Compound interest, to be specific. If the number of times that  interest is compounded is so much that it’s almost infinity, that’s  where you see e.

You  think I’m making this up but all of this is real. Although, some parts  are imaginary, like the number i. Don’t get me wrong. It exists. The  number i is just the term we use for the square root of -1.

One day, someone said:

“I wonder what number when multiplied by itself gives us -1?”

and then i was born.

How did you discover Euler’s Identity?

I was studying Mathematics in college. It’s  funny because I had a really strong passion for Math, but I didn’t  really have an understanding of how much Mathematical ideas can connect  to one another, and I hadn’t taken any advanced courses yet.

Anyway,  I saw this equation typed out on a piece of printer paper and taped to  the outside of someone’s door. I stood there, read the equation, and I  remember being simultaneously shocked and humbled at the same time.

My first thought was:

“Wow, this is incredible that these numbers are all related.”

and then I started thinking:

“How can I be studying Math and not know about this? I have so much to learn, and I want to learn more!”

These  numbers come from fields of math that seem so different — The numbers 0  and 1 from arithmetic, Pi from geometry, e from finance, and i from  algebra. I find it interesting that they all have a relationship that  can be summed up in one simple sentence. It’s poetic in a way.

Studying  all of these different kinds of math in school, I had no idea these  separate ideas were all connected. That’s what I love most about math.  That it’s all connected in some  way. Even things that we think today might not have a connection. Well,  it might be because we haven’t discovered the connection yet.

Why do you think Euler’s Identity is important?

It’s  important because it shows the beauty of pure mathematics. When  debating the importance of mathematics with my husband — yep, we have  those conversations in our household! — I have this beautiful equation  to cite. It’s proof that mathematics can be beautiful in its own way,  without needing to be a tool for science or engineering, which is how,  understandably, my aerospace engineer husband sometimes sees it.

Can you tell us about the history of it?

I’d love to! It’s a fascinating history that really began long ago. You  see, as people first began to count they developed the concepts of 1  and 0… something and nothing. And you see those concepts in their  written form across ancient cultures across the world. They are a part  of our human existence. Even our very recent history wouldn’t be  possible without the concept of 1 and 0 — the only numbers necessary for  computers!

The  concept of Pi has also been around for a while. In a practical sense,  ancient civilizations understood that there was a relationship between a  circle’s circumference and its diameter. Although a crude  approximation, they did use it to measure and construct… whatever  circular things they needed to construct. It  wasn’t until much later, when mathematics extended beyond just the  practical into an abstract realm of its own, that we realized all the  other applications of Pi.

The  concepts of i and e are much more recent in human history. Probably  because of their abstract nature. We needed a new set of numbers to  describe the things we were pondering, like the side length of a square  with a negative area. The number i and it’s imaginary friends came out  of that.

As  I mentioned earlier, the number e came about with the introduction of  compound interest in society, which is also a fairly modern human  concept. However, Leonard Euler (and a few other notable  mathematicians of the time) discovered its connection to trigonometry  and imaginary numbers sometime around the 18th century. And then this  remarkable connection was made between the great numbers 0, 1, pi, i,  and e in Euler’s Identity.

I’m terrible with the exact dates and names on all of this. In  fact, it’s pretty difficult to attribute anything mathematical to just  one mathematician at one point in time because throughout history great  Mathematicians have worked together. Many great discoveries can be  attributed to several people at several points in time. It’s truly  fascinating! Kind of makes you think that it’s part of a greater truth,  and we are just uncovering it.

Enough about the past! How do you think it will be useful in the future?

I don’t know. Nor do I really care!

Don’t get me wrong, I care about the future. And I think it’s great when math is useful. But I don’t think math equations have to be useful to be important. Kind of like great pieces of art. We don’t judge the Mona Lisa based on its ability to identify a woman…possibly named Lisa. That’s absurd!

Anything else interesting to add?

Well,  I am interested in seeing what kinds of other remarkable connections  exist that we just haven’t uncovered yet. Or even practical applications  to math that we think is entirely abstract at the moment. That will be  exciting!

Oh and one more thing… I haven’t revealed why Euler’s Identity is true. You’ll have to look it up to find out!

Keen to read more from the Coffee + Math series? Check out our last post in which we use stats to prove that it’s possible to make an infinite amount of money!